Die Funktion ax^3 +bx^2+cx+d mit ganzzahligen Koeffizienten ABC & D hat die angegebene Null Stellen bestimmen Sie A, B. C. & D?
Kann jemand vielleicht als Beispiel die b machen

4 Antworten
Hier hast du eine Funktion mit 3 Parametern bzw. Koeffizienten (A,B,C). Du hast 3 Nullstellen gegeben , also Werte, bei denen der y-Wert gleich 0 ist (f(x)=0). Somit sind die x- und y- Werte bekannt.
Du kannst diese also jeweils in die Funktion einsetzen und bekommst somit 3 Gleichungen. Jetzt hast du somit 3 Gleichungen und 3 Unbekannte. Dadurch ist dies auflösbar.
Ab hier gibt es verschiedene Möglichkeiten das Gleichungssystem zu lösen. Man kann z.B. das Additionsverfahren, Gauß-Verfahen oder Einsetzungsverfahren oder ein Mix aus diesen verwenden.
Zum Rechnen bin ich derzeit zu faul.
f(x) = a*(x+1/3)(x-3)(x-10/3)
wobei das a der gesuchte Parameter ist
.
(x+1/3)(x-3)(x-10/3) = x³ - 6x² + 71/9 x + 10/3
Der gemeinsame Nenner von 9 und 3 ist 9
Alles mal 9

fertig
mit a = n*9 und n aus Z ( außer 0 ) erhält man alle Lösungen
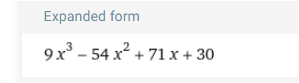
f(x) =a(x+1/3)(x-3)(x-10/3)
Die Konstante ist zunächst 10/3. a könnte also 3 sein , d dann 10, den Rest kannst du machen.
Tipp: Mit 3 Nullstellen lassen sich keine 4 Parameter eindeutig bestimmen. Daher gibt es unendlich viele solche Funktionen der Form
Du brauchst also noch die Bedingung "ganzzahlig". Wenn Du den Ausdruck ausmultiplizierst, kannst Du diese Bedingung noch verwenden, um die Koeffizient ganzzahlig zu machen.
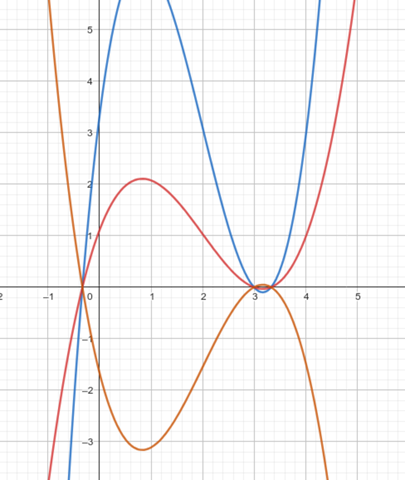
Skizze:
blauer Graph: e = 1
roter Graph: e = 1/3
oranger Graph: e = -1/2