Welche er beiden Basen ist richtig bzw. spannt den Unterraum auf?
Bisher hatten wir gelernt, dass die Basis U alle lin unabhängigen Vektoren, die durch Anwendung des Gauß Algorithmus entehehen. Also sozusagen (1,0,0) (0,1,0) (0,0,1) z.b
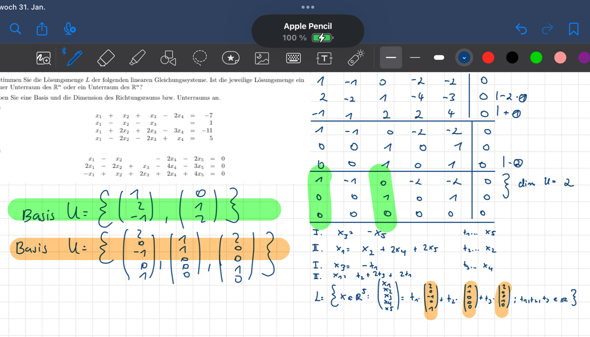
in unserem Beispiel ist es aber so bzw. in der Lösung steht, dass die Basis U = die Vektoren sind aus der lösungsformel (im Bild unten rechts)
Was ist jetzt richtig. Gerne mit Erklärung. Danke :)
1 Antwort
Die Lösungen des LGLS sind natürlich Elemente des Grundraumes ℝ^5.
Also müssen auch die Basiselemente des Lösungsraums der homogenen Gleichung aus dem ℝ^5 stammen.
Allenfalls könntest du die Matrix um zwei Nullzeilen ergänzen, um eine 5x5-Matrix zu erhalten. Aber auch die Spaltenvektoren dieser Matrix sind nicht unbedingt Lösungsvektoren - es wird ja das Skalarprodukt eines Zeilenvektors dieser Matrix mit einem Lösungsvektor als Spaltenvektor gebildet, um auf eine Koordinate des Zielvektors zu kommen.
(Ich frage mich auch, wieso das von dir genannte Verfahren funktionieren sollte - die ursprüngliche Form des LGS ist ja in keiner Weise gegenüber Umformungen ausgezeichnet, die Form nach der letzten Umformung müsste also ebenso gut geeignet sein.)
Der Rang des Gleichungssystems ist 2 (es lässt sich so umformen, dass 2 (Zeilen-)Vektoren ungleich Nullvektor übrig bleiben aber nicht weniger) - das ist natürlich auch der Rang der zugehörigen Matrix. Und dieser Rang ist die "Defektdimension", also die Differenz zwischen den Dimensionen von Gesamtraum (5) und Lösungsraum (3). Bzw. kann man aus dem Rang des LGS (2) auf die Dimension des Lösungsraums (3) schließen: 3 = 5 - 2
Eine Basis findet man z. B. wie hier, indem man so viele Koordinaten der allgemeinen Lösung (des homogenen LGS) durch andere Koordinaten ausdrückt, dann kann man die übrig gebliebenen Koordinaten durch die Parameter ersetzen.