Warum wird man immer schwerer, je schneller man sich bewegt?
Das geht bei hohen Geschwindigkeiten ja aus irgendwelchen Gleichungen von Einstein hervor. Ist das einfach nur eine hergeleitete Erkenntnis aus einer Gleichung oder lässt sich das auch irgendwie anschaulich erklären?
5 Antworten

Hallo 0Meeri7,
man schleppt gewissermaßen seine eigene kinetische Energie mit, und die "wiegt was". Das wird durch EINSTEINs berühmte Formel
(1) E = mc²
ausgedrückt. Sie bezieht sich auf die Erkenntnis, dass die scheinbar ganz unterschiedlichen physikalischen Größen Energie E und Masse m in Wirklichkeit eine einzige sind, nur dass sie im SI in unterschiedlichen Maßeinheiten gegeben sind.
- Jegliche Energie, auch die kinetische Energie Eₖ, "wiegt was".
- Die Masse m eines Körpers oder Teilchens ist physikalisch mit ihrer Ruheenergie E₀ identisch.
Genauer als (1) ist daher
(2.1) E₀ = mc²
(2.2) E = E₀ + Eₖ = E₀/√{1 − (v⁄c)²} =: mc²γ
Hinzu kommt noch die Formel für den Zusammenhang zwischen der Energie und dem 1D-Impuls p›:
(3 1) (E⁄c)² = (E₀⁄c)² + p².
Fortbewegung ist relativ; um sinnvoll von ihr zu sprechen, brauchen wir einen Bezugskörper, einen Körper B, den wie als stationär ansehen. Ein von B aus definiertes raumzeitliches Koordinatensystem Σ heißt dann auch ein Bezugssystem.
B kann z.B. ein Raumfahrzeug mit ausgeschaltetem Antrieb sein.
Wenn Du in einem anderen, ebenfalls nicht angetriebenen Raumfahrzeug B' mit konstanter 1D-Geschwindigkeit v (in x-Richtung von Σ) mit, sagen wir, 0,6c an B vorbei gleitest, ist γ=1,25, d.h. Nehmen wir der Einfachheit halber an, beide Raumfahrzeuge seien baugleich.
Du schleppst quasi ein zusätzliches Viertel Deiner Ruheenergie als kinetische Energie mit – in Σ. In einem von B' aus definierten Koordinatensystem Σ' ist nicht B in Ruhe, sondern B', und B bewegt sich mit −v (gleiches Tempo, entgegengesetzte Richtung) an Dir vorbei. Daher ist in Σ' B um 25% "schwerer", d.h. schleppt gleichsam 25% seiner Ruheenergie als kinetische Energie mit sich.
Welches Raumfahrzeug als "schwerer" gilt, ist also Interpretationssache.
Tatsächlich lässt sich die E⁄c auch als "Impuls in Zeitrichtung" auffassen, der zusammen mit den räumlichen Impulskomponenten den Viererimpuls bildet. Das Quadrat seines "Betrages" ist
(3.2) (E₀⁄c)² = (mc)² = (E⁄c)² − p².
Diese Abwandlung des Satzes des PYTHAGORAS heißt auch MINKOWSKI- Länge und ist für Vierervektoren typisch.
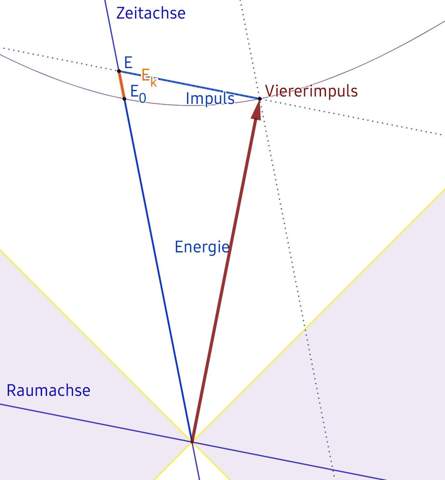
Abb. 1: Der Viererimpuls


Ist das einfach nur eine hergeleitete Erkenntnis aus einer Gleichung
"nur" ist gut. Das ist der beste direkte Zugang zur Theorie. Aber zuerst die Lichtgeschwindigkeit: Die sogenannte Lichtgeschwindigkeit ist die Geschwindigkeit, mit der Realität sich ausbreitet. Nichts was Ruhemasse* hat kann diese Geschwindigkeit erreichen, und nur weil Photonen keine Ruhemasse haben, haben sie diese Geschwindigkeit, daher der Name.
Der Name kommt auch daher, dass man früher glaubte, das Licht brauche ein absolut stationäres Medium, in dem sich elektromagnetische Wellen ausbreiten (so wie Schallwellen in Luft), den sog. Äther. Die Frage, woran so ein stationärer Äther räumlich festgemacht sei, führte zum Michelson-Morley Experiment, bei dem eigentlich erwartet wurde, dass mit der Geschwindigkeit der Erde durch den Äther unterschiedliche Geschwindigkeiten des Lichts in unterschiedliche Richtungen gemessen würden. Überraschung: kein Unterschied, also kein Äther (es sei denn er würde zufällig ausgerechnet an der Erde festgemacht sein). Daraus geht nicht nur hervor, dass es keinen Äther gibt, sondern dass diese Geschwindigkeit eine in allen Inertialsystemen gleiche Naturkonstante und damit nicht überholbar ist, denn wenn man versucht den Strahl einer Taschenlampe mit dem Auto zu überholen, ist er relativ zum Auto genauso schnell wie relativ zur Taschenlampe.
Erst hier setzt die spezielle Relativitätstheorie an, die mit recht einfacher Mathematik (Lorentz-Transformationen) darlegt, was das für Auswirkungen auf Zeiten und Längen (und auch die kinetische Energie*) in bewegten Systemen hat.
*) Kinetische Energie von Objekten mit Ruhemasse enthält einen Term der Lorentz-Transformation wie Zeiten und Längen. Wenn man ein Fahrzeug in die Nähe der Lichtgeschwindigkeit beschleunigt, geht mit wachsender Geschwindigkeit ein immer größerer Anteil der zugeführten Energie in immer weniger Geschwindigkeitszuwachs und lässt für den äußeren Beobachter das Fahrzeug immer träger erscheinen - die Lichtgeschwindigkeit wird nie erreicht.

Die Lichtgeschwindigkeit ist absolut (vergl. Relativitätstheorie) und für Materie mit Ruhemasse nur annäherungsweise erreichbar, da der Energieaufwand zur Beschleunigung gegen unendlich tendiert.
Die zu beschleunigende Materie verschlingt mit steigender Geschwindigkeit immer mehr Energie, so als würde die Masse zunehmen, was jedoch nicht bildlich zu verstehen ist.
Korrekt ausgedrückt nimmt die kinetische Energie der beschleunigten Materie zu und wäre bei (der unmöglich zu erreichenden) Lichtgeschwindigkeit unendlich.

Wir reden hier nicht von Gewicht sondern Kraft. Aber ja im Prinzip kann man es auch als Gewicht vorstellen.
Stell dir ein Fahrrad vor. Die kraft wird von deinen Beinen über die Pedale und dann zum Hinterrad geleitet was eine Vorwärtsbewegung zur Folge hat. Du tauschst deine Kraft gegen Bewegungsenergie. Je kräftiger du in die Pedale trittst desto schneller wirst du.
Als nächstes Stell dir vor du fährst gegen eine Glasscheibe. Einmal im Schritttempo (ca. 5 km/h) und einmal volle Pulle (ca. 40 km/h)
Um Schritttempo zu erreichen brauchst du nicht viel Kraft. Die Scheibe bleibt also beim Aufprall ganz.
Um 40 km/h schnell zu sein musst du viel Kraft aufbringen. Diese gesamte Kraft wirkt dann beim Aufprall auf die Scheibe. Die Scheibe zerbricht also.
Ich kann dir das ganze auch noch mit Physikalischen Einheiten und Formeln erklären wenn du möchtest.

Nein, aus der Gleichung geht hervor, dass die benötigte Energie exponentiell mehr wird, je schneller man sich bewegt. Bei Lichtgeschwindigkeit wäre sie unendlich, somit ist diese Geschwindigkeit nicht erreichbar. (Eine Theorie gilt solange, bis etwas anderes bewiesen ist)