Quadratische Funktionen Flugbahn Parabel, höchster Punkt (S) berechnen?

Hallo, ich bekomme bei meiner Aufgabe die Nr. 14b leider nicht ausgerechnet. Ich weiß nicht mit welcher Formel ich den Scheitelpunkt (S) berechnen muss. Vielen Dank :). Lg

Answer 1

[lolala00932020]

Um den Scheitelpunkt einer Parabel zu berechnen, kannst du die allgemeine Formel für die Scheitelpunktform verwenden. Die Scheitelpunktform lautet:

S(x, y) = (h, k)

Die Werte von h und k können mit den folgenden Formeln berechnet werden:

1. Der x-Wert des Scheitelpunkts (h) wird berechnet, indem du die Gleichung
2. h = -b / (2a)
3. verwenden, wobei a, b und c die Koeffizienten der allgemeinen quadratischen Gleichung in der Form ax^2 + bx + c = 0 sind.
4. Der y-Wert des Scheitelpunkts (k) wird berechnet, indem Sie den Wert von h in die ursprüngliche quadratische Gleichung einsetzen:
5. k = f(h) = ah^2 + bh + c

Comments

[Scharfechilli]

Dankeschön 🙏

Answer 2

[evtldocha]

Ich an Deiner Stelle würde den x-Wert des Scheitelpunkts aus dem Mittelwert der Nullstellen ermitteln (Der Scheitelpunkt einer Parabel befindet sich in der Mitte der beiden Nullstellen):

$-\frac{7}{1000}x\cdot\left(x-\frac{9}{10}\cdot\frac{1000}{7}\right)=0\ \rightarrow\ x_1=0:\ x_2=\frac{900}{7};\ x_s=\frac{900}{14}$

Von hier aus ist es dann nur noch ein kleiner Schritt bis zur maximalen Flughöhe.

Skizze:

Comments

[Scharfechilli]

Hallo, vielen vielen Dank 😊

Answer 3

[Tannibi]

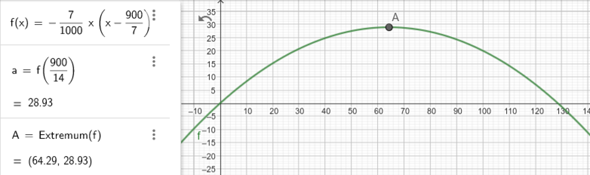
Du hast sicher f(x) als Funktionsgleichung
identifiziert. Dann klammerst du aus:

x (-0.007x + 0.9) = 0
-0.007x + 0.9 = 0
-0.007x + 0.9 => x = -0.9/-0.007 = 128.6 (zweite Nullstelle)

Der Scheitelpunkt liegt in der Mitte dazwischen, also bei 129.6/2 = 64.8 m

Comments

[Scharfechilli]

Vielen Dank für die Hilfe, dass bringt mich weiter :)