Mathe-Rechenaufgabe Öltank?
Kann mir jemand bei folgender Aufgabe zur Trigonometrie helfen:
Ein zylindrischer Öltank, dessen Achse horizontal liegt, ist 4,00 m lang, sein Grundkreis besitzt den Durchmesser 1,60 m. Die Messung mit einem Messstab ergibt, dass der Flüssigkeitsspiegel 1,00 m hoch steht.
a)Wie viel Öl ist noch im Tank?
b) Wie viel Prozent der Gesamtfüllung sind das?
5 Antworten
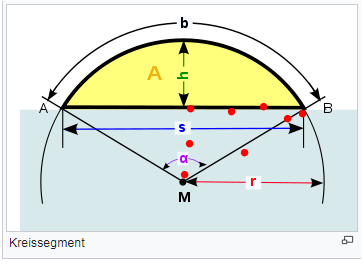
Zuerst s/2 bestimmen, danach den Mittelpunktswinkel alpha, dann den Flächeninhalt
.
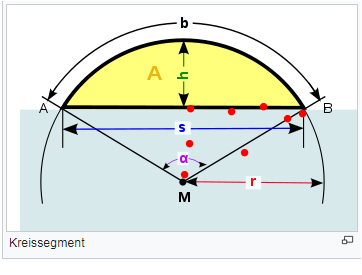
Das Volumen eines Zylinders berechnet sich so :
Volumen = pi mal r hoch 2 mal die Höhe . Da der Zylinder liegt ( horizontal ) hat er 4 m ; der Radius ist die Hälfte vom Durchmesser 0,8 m , pi ist 3,14...
V = 3,14 .. mal 0,8m mal 0,8 m mal 4 m = 8,04 qm , das sind 8040 l Gesamtvolumen
Die Hälfte snd 4020 Liter ( 0,8 m Radius ) ; gefragt sind 1 Meter ; also noch ein Viertel dazu ergibt 5025 Liter zu a )
8040 Liter zu 5025 Liter ergibt = 62,5 % der Gesamtfüllung
Ganz sicher bei den letzen beiden bin ich mir nicht .
Hier findest Du alle Formeln
https://de.wikipedia.org/wiki/Kreissegment
Du kennst h (1m) und r (1,6m/2)
α rechnest Du mit:
α = 2 ∙ arccos(1 - h/r)
A ist dann
A = r²/2 ∙ (α - sin(α))
Dieses A ist die Fläche des Kreissegmentes über dem Öl ("Luftfläche")
Für die "Ölfläche" mußt Du die "Luftfläche" von der Kreisfläche (π∙r²) abziehen.
Ölfläche / Kreisfläche ist der Füllgrad des Tankes
Für das Volumen multiplizierst Du die "Ölfläche" mit der Tanklänge.
Du hast recht, damit ist es einfacher und man erspart sich den Weg über "Luft-"/"Ölfläche"
Das sollte dir weiterhelfen


Ich hoffe das hilft dir :)
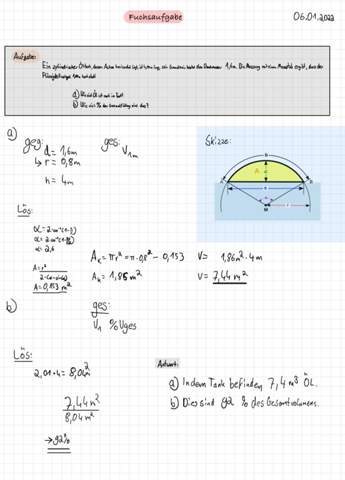
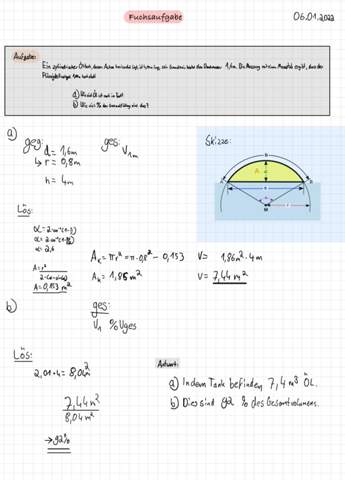
Bis 4020 l ok, aber dann darfste nicht einfach proportional zur Ölstandshöhe weiterrechnen, der Querschnitt ist ja nicht rechteckig...