Lineare Algebra Gaußschen Eliminationsverfahren?

Hallo zusammen,

ich soll mit diese Punkte eine Ausgleichgerade und Parabel erstellen:

Punkte: (1, 4), (3, 7), (4, 15), (7, 21), (10, 15)

y1= a+b*x

y2= a+b*x+c*x^2

Hier sind meine Lösungen:

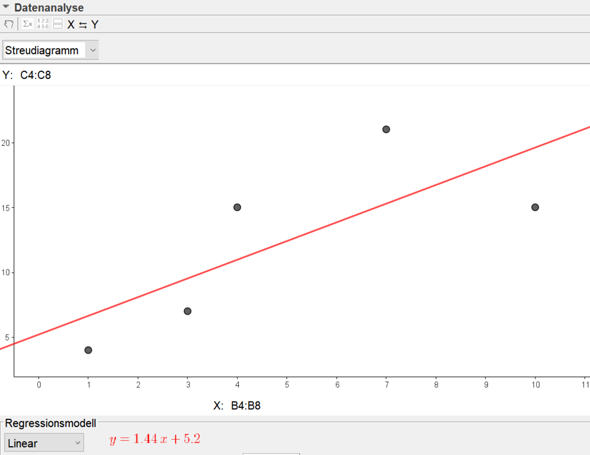
Y1= 5.2+1.44x

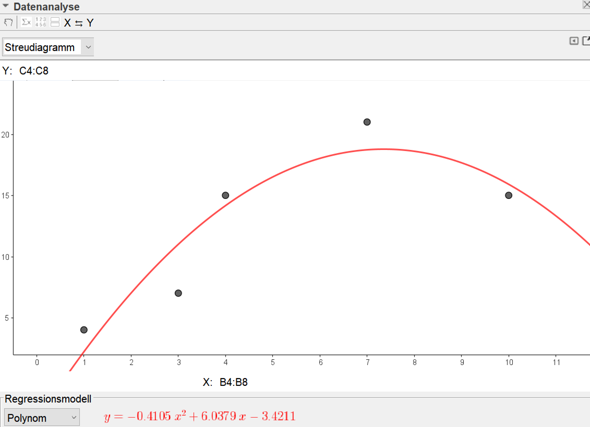
y2= -6.98+7.94x-0.58x^2

ich soll überprüfen, ob die Ausgleichsgerade und die Ausgleichsparabel so durch die vorgegebenen Punkte verlaufen, so dass die senkrechtenAbstände zu den Punkten relativ gering sind.

Meine gerade und Parabel verlaufen nicht durch die punkte, ist das in Ordnung?

Answer 1

[Genuatief]

ich bekomme für die lineare Regression das selbe:

Für die quadratische aber das:

Was meinst du mit

 dass die senkrechtenAbstände zu den Punkten relativ gering sind.

??

Bei einer Standard-Regression macht man die Summe der quadratischen Abweichungen minimal. Was hast du gemacht?

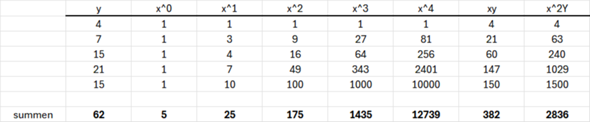
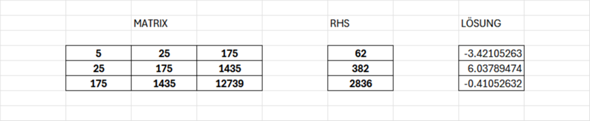
Da komme ich aber genau auf meine Zahlen:

Ergänzung:

Zahlen:

Matrix-Gleichung:

Comments

[Hana09]

dass die senkrechtenAbstände zu den Punkten relativ gering sind. So steht es in der Aufgabe , habe es auch nicht verstanden. Mein Graph sieht auch so aus

[Genuatief]

@Hana09

musst halt zeigen, was du gerechnet hast

[Hana09]

@Genuatief

Hab zu der Aufgabe hinzugefügt

[Genuatief]

@Hana09

ich hab in meiner Antwort die Rechnung ergänzt. Du hast irgendwo einen kleinen Fehler in deiner Rechnung. Ich komme mit deinen Matrixgleichungen genau auf meine obige Lösung.