4. Dimension?
Hallo,
ich habe eine Frage zur 4. Dimension. Ich kann mir das nicht so ganz vorstellen und habe mir deshalb ein Modell in 3D gebastelt. Jetzt meine Frage: Stimmt dieses Modell auch oder ist da ein Fehler drin? Ich habe zuerst zwei Würfel aus Schaschlik Spießen gebastelt. Dann habe ich diese zwei Würfel ineinander gesteckt und mit acht weiteren Schaschlik Spießen verbunden.
Vielen Dank für eure Antworten!

6 Antworten
Bis auf den einen fehlenden Spieß stimmt, was du gemacht hast.
Allerdings hast du keinen 4D-Würfel gemacht, sondern nur die 3D-Projektion eines 4D-Würfels. Was anderes geht ja auch nicht, es sollte nur klar formuliert werden.
Da es eine Projektion ist, sind auch die Darstellung mit neben- oder ineinander liegenden Würfel gleichwertig, sie ergeben sich dadurch, dass man die Projektionsrichtung ändert. Beim Schatten eines 3D-Würfels auf einer 2D-Leinwand kannst du auch alle möglichen Anordnungen erzeugen, je nach Lage von Lichtquelle, Würfel und Leinwand.
Sagt man nicht, die 4 Dimension wäre die Zeit?
Wie können uns an der X-, Y- und Z-Achse vor und zurück bewegen, die Zeit verläuft für uns zwar nur in eine Richtung, jedoch bewegen wir uns in ihr.
Da stellt sich dann natürlich die Frage ob wir 3,5 dimensional sind, aber gut, ich denke das passt erstmal so.
Joa, ergibt Sinn. Es soll ja sehr viele Dimensionen geben. Man lern nie aus.
Gebe jedem deiner Eckpunkte eine Adresse mit 3 Koordinaten, dann wirst du bald feststellen, dass du nur dreidimensionale Positionen im Raum beschreiben kannst. Auch wenn du eine vierte Koordinate zur Verfügung hättest, stellt sich die Frage, welche Richtung sie definieren sollte, die sich nicht auch mit den anderen drei Dimensionen beschreiben lässt.
Eine 4D-Adressierung ist recht leicht zu verstehen, wenn du dir einfach nur vorstellst, dass jede Dezimalstelle eine Dimension darstellt. Wenn dann z.B. die maximal mögliche Zahl 999 ist, dann wären drei Dezimalstellen (3D) nötig, um alle möglichen Zahlen darzustellen.
Wenn aber die maximale Zahl größer als drei Stellen ist, wie z.B. 9999 (4D), dann kann die 4. Stelle nicht erkannt werden, weil du nur 3 Dezimalstellen erfassen kannst. Daher ist 239 nicht vergleichbar mit 5239, weil sie sich mit der 4. Dezimalstelle signifikant unterscheidet, was wir aber in unserem 3D-Universum optisch nicht wahrnehmen, denn andere Wirkungen werden nicht erwartet und daher auch nicht festgestellt.
Vielen Dank für dein Beispiel mit den Ziffern! Meinst du also, man kann die vierte Dimension nicht darstellen, weil es bei uns nur bis 3D geht? Aber man kann ja auch einen 3D-Würfel auf ein 2D-Blatt zeichnen.
Das nennt man dann 3D-Differenzialgeometrie. Wenn man aber einen Tesserakt zeichnet, der gerne auch als 4D-Würfel verstanden wird (was aber Unfug ist), wie du hier unter diesem Link sehen kannst, dann musst du das nur mit der Kugel vergleichen und siehst dann, dass das Innere auch gleichzeitig außen ist. Doch solche Zusammenhänge werden nur mathematisch mit einer 4D-Differenzialgeometrie gelöst, aber du siehst und erlebst immer nur die 3D-Version, weil eben hier auf unserer 3D-Ebene keine 4. Dimension darstellbar ist, denn du siehst immer nur die 239 von der 5239.
Der Tesserakt sieht, soweit ich das erkennen kann, gut aus - üblicherweise steckt man allerdings die beiden Kuben ineinander…

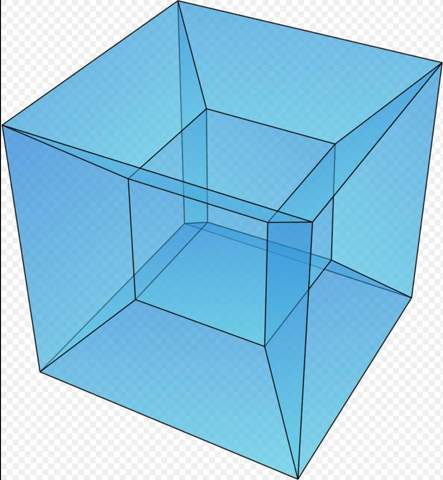
Dankeschön! Weißt du auch, warum man die Würfel üblicherweise ineinander steckt?
Das ist das sogenannte Schlegeldiagramm, das topologische Eigenschaften invariant lässt, jedoch nicht längen- und winkeltreu ist…
Weil es so eventuell "übersichtlicher" bleibt. Eine komplett maßstabsgetreue Abbildung eines 4D-Würfels in den 3D-Raum ist ohnehin unmöglich.
Was du mit deinem "Schaschlik-Würfel" darstellst, ist eine Art Projektion eines 4D-Superwürfels in den 3D-Raum. Ganz analog benützen wir ständig Projektionen von 3D-Objekten auf den 2D-Raum einer Ebene, indem wir sie in der Art und Weise eines Grundriss-Plans oder auch etwa durch eine Fotografie darstellen.
Nein. Zeit ist eine Dimension. Die sind nicht durchnummeriert. Ich kann auch mit 10 oder 100 Raumdimensionen rechnen.