Winkelgescgwindigkeit Bahnverhältnis?
Hey,
folgende Frage.
Nehmen wir an, zwei Planeten bewegen sich um ein Stern und die Planeten stehen alle 2,05 Jahre in einer Linie, kann man daraus irgendwie die Winkelgeschwindigkeit berechnen? Also durch die Bedingung, alle 2,05 Jahre in einer Linie zu stehen.
die Planeten stehen alle 2,05 Jahre in einer Linie
2 Planeten (mathematisch 2 Punkte) liegen IMMER auf einer Geraden.
Du meinst vmtl, alle 3 Himmelskörper liegen auf einer Geraden.
Ja
5 Antworten
Man kann nur die Differenz der beiden Winkelgeschwindigkeiten angeben.
Sei omega2>omega1 und T die kürzeste Zeit zwischen den beiden Anordnungen, wo die Körper in der gleichen Reihenfolge auf einer Geraden liegen.
Dann gilt für eine natürliche Zahl n
Dies ist die einzige hinreichende und notwendige Bedingung.
Bitte entschuldige, ich muss mich korrigieren. Hab zu wenig überlegt, was ich oben geschrieben habe war nicht ganz korrekt. Leider kann man in den Kommentaren offenbar keine Formeln schreiben.
Also nochmals:
Sei omega2>omega1. Dann muss gelten:
omega1 T=2*n1*pi
omega2 T=2*n2*pi
omega2-omega1=2*(n2-n1)*pi/T
Damit T die kürzeste Zeit für die Konstellation der Körper auf einer Geraden mit gleicher Reihenfolge ist, müssen n1 und n2 teilerfremd sein (z.B. n1=3, n2=7).
Wenn omega2/omega1 irrational ist, wird die Konstellation höchstens einmal auftreten.
Könntest du dir meine Privatnachricht anschauen?
Sorry, war immer noch nicht allgemein genug. Die Planeten müssen ja nicht notwendigerweise immer beim gleichen Winkel auf einer Geraden liegen.
Also muss für eine natürliche Zahl n gelten
omega1*T = phi
omega2*T = phi+2*n*pi
Wenn T die kürzeste Zeit zwischen zwei derartigen Konstellationen ist, gilt n=1 (nach der Zeit T hat der schnellere Planet den langsameren quasi einmal überrundet). Also muss gelten
omega2-omega1 = 2*pi/T
Die Bedingung in der ersten Antwort sollte also korrekt gewesen sein.
Warum jetzt +2 ?
Könntest du mir vielleicht erklären, was du da genau ausrechnest, bzw, inwiefern das eine Bedingung ist: dj sagst ja: die Winkelgeschwindigkeit mal die Zeit ist seine Strecke
Und beim zweiten: die vorherige Strecke (vom ersten Planeten) +2 mal n (n steht eine Zahl, aber was soll da rein) × pi isz die andere Strecke. Aber wieso?
Woher kommt die 2 und wofür steht das N? (Für doppelt so viel gleich in einer Linie??)
Nach einer Zeit T sollen die Planeten wieder auf einer Geraden liegen, und zwar in der gleichen Reihenfolge. In dieser Zeit habe der äussere Planet den Winkel phi zurückgelegt. Damit die Planeten wieder auf einer Geraden liegen, muss der innere Planet einen Winkel phi+2*n*pi zurückgelegt haben, also phi plus n ganze Umrundungen.
Ist T die kleinste Zeit zwischen zwei derartigen Konstellationen, muss n=1 gelten (denn falls n ungleich eins wäre, träte schon beim Winkel phi/n zur Zeit T/n die gleiche Konstellation auf).
Subtrahiert man die beiden Gleichungen
omega1*T=phi
omega2*T=phi+2*pi
ergibt sich
omega2-omega1=2*pi/T
Meiner Meinung nach kann man allein aus diesen Angaben keine Rückschlüsse auf die Winkelgeschwindigkeit ziehen.
Stell dir vor, der äußere Planet ist "unendlich" weit weg vom Stern, er braucht "unendlich" lange, um den Stern zu umrunden, das heißt, er steht praktisch still.
Wenn nun alle 3 Körper immer 2,05 Jahren auf einer Linie stehen, so bedeutet das, der andere Planet braucht genau 2,05 Jahre für eine Umdrehung.
Nimmt man den äußeren Planeten nun näher an, so bewegt auch er sich um den Stern, der Innere Planet muss also eine volle Umrundung schaffen PLUS den Winkel, den der andere Planet in den 2,05 Jahren überstrichen hat.
Die Winkelgeschwindigkeit ist damit eine völlig andere.
okay und was wenn die Umlaufbahnen ein Verhältnis von 1,4 teilen
... dann hast Du auch ein Verhältnis für die Umlaufzeiten (3. Keplersches Gesetz) und damit kannst Du dann die Gleichung aus der Antwort von Clemens1973 lösen.
Ich kenne das dritte keplersche Gesetze aber verstehe noch nicht so ganz, inwiefern ich das in Clemens Gleichung einsetzen kann (weil ich die +1 nicht ganz versteh/warum ausgerechnet +1). Ich wäre dir sehr dankbar, wenn du mir das vielleicht vorrechnen könntest.
Ich habe mal eine eigene Antwort geschrieben. Vielleicht macht es das klarer.
Antwort nach Nachfrage zu einem eigenen Kommentar.
Vielleicht hilft die Skizze hier (Indices mit "ä" beziehen sich auf den äußeren Planeten und analog Indices mit "i" auf den inneren Planeten):

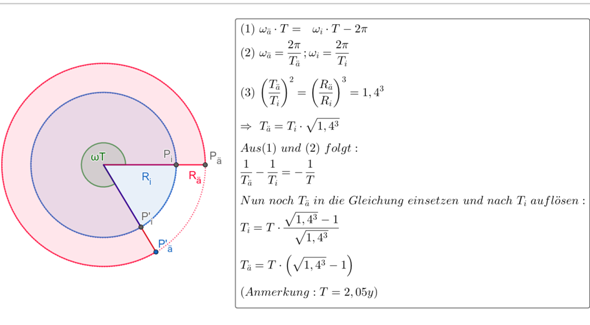
Okay aber eine Frage habe ich doch noch, ich bin alles durchgegangen und verstehe nicht wie du den oberen Term so umgeformt hast, dass du rausbekommen Ti= T Wurzel...
Könntest du mir das zeigen, ich wäre dir sehr dankbar!
Auf die Ti bin ich gekommen könntest du mir jedoch bitte zeigen, wie du auf die Umformung mit Ta gekommen bist?
Hey,
Erstmal schöne Veranschaulichung.
Alles scheint mit sehr logisch nur der erste Schritt nicht: warum subtrahierst du bei der Gleichsetzung T- 2pi? 2pi wegen einer Umdrehung, aber wieso minus, der innere Planet ist ja nicht genau 1 mal mehr rotiert (das weiß man ja nicht). Zudem: wenn die Planehen mit dem Stern in einer Linie stehen, gibt es zwei Möglichkeiten:
Gegenüber und nebeneinander
Weil wenn wir von nebeneinander ausgehen, dann können wir ja die 2pi nehmen bei gegenüber reichen doch aber auch pi, oder?
Mit -pi würde man ja ausdrücken, dass die Planeten gegenüber stehen,2pi dann nebeneinander, was ist aber der Unterschied zu + pi/2pi
Weil sagen wir mal nach 2,05 stehen die Planeten gegenüber, dann müsste ich ja für die Gleichsetzung -pi rechnen. Das heißt ja, wenn ich den Ausdruck -2pi wähle, dass ich den Zeitpunkt wählen muss, wann die Planeten nebeneinander stehen, oder?
Und wieso ausgerechnet 2pi und nicht 4 oder 6pi ? Es macht ja ansich keinen Unterschied oder? (Vom Zahlenwert )
-> wegen der geringsten benötigten Zeit t, ich verstehe , aber warum -pi?
Vergiss alle meine Kommentare, ich habs verstanden:
Eine Sache jedoch trotzdem:
Wenn wir wie du es gemalt hast das Szenario Planet Planet Stern haben sind es
Sagen wir das passiert alle 3 jahre
Omega 1 x T = Omega 2 x T -2pi
Wenn wir aber das Szenario
Planet Stern Planet miteinbeziehen, dann hätten wir Omega 1 x T = Omega 2 x T -pi
Das ist ja eine Periode und die Szenarien wiederholen sich ständig (periodisch).
Wenn wir aber für beide sagen, dass ws alle 3 Jahre passiert. Dann würden doch beide Ausdrücke verschiedene Winkelgeschwindigkeiten (weil anstatt 2pi -pi) haben, oder bin ich da falsch?
mach dich bitte mal mit den 3 "keplerschen gesetzen der himmelsmechanik" vertraut, google hilft.
die winkelgeschwindigkeit wird in einem der 3 genau definiert.
Nein.
Hey,
Ich möchte diese Bedingung nachvollziehen.
T x Winkelgescheindigkeit-> zurückgelegte Strecke (x n ist die Strecke, eines Planetens, damit er auf einer Linie mit den zwei anderen Himmelskörpern steht). Ich verstehe auch, dass die zurückgelegte Strecke des äußeren Planetens größer sein muss (+1), aber warum ausgerechnet 1? Und was sagt die Rechnung w2-w1 im Sachkontext aus (inwiefern ist das eine Bedingung)?