wie kann ich die Schnittpunkte zwischen den beiden funktionen berechnen?
Hey Leute wie kann ich die Schnittpunkte zwischen den beiden Funktionen berechnen?
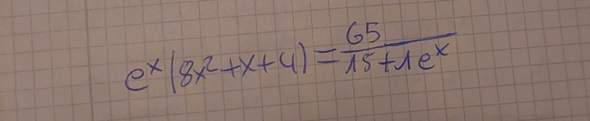

Sind die Terme auf beiden Seiten der Gleichung die Funktionsterme?
Was ist das Zeichen vor dem e^x rechts im Nenner?

Ja beides sind Funktionterme also Funktionen die sich schneiden. Das vor dem e^x ist eine 1 die könnte man also auch weg lassen.
4 Antworten

Mit der Macht des Newtonverfahrens...
oder der Weight Lambert W-Funktion (Umkehrfunktion von x + ln(x).
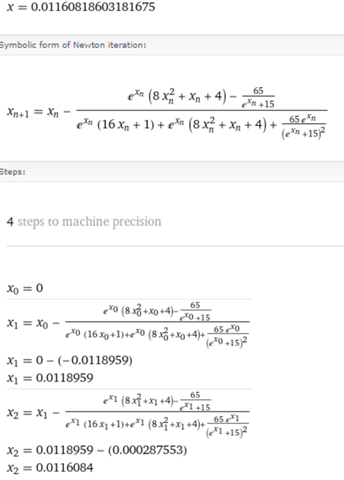
Erstes Ergebnis
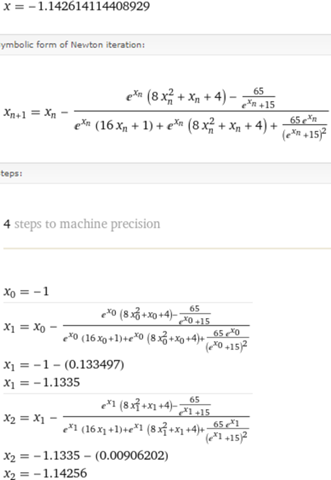
Zweites Ergebnis
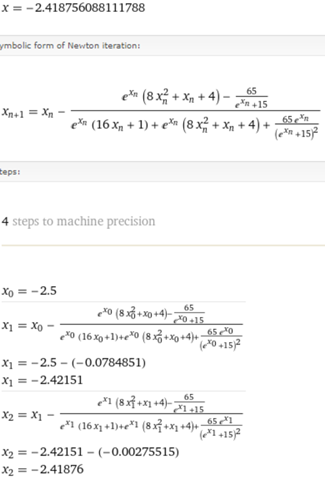
Drittes Ergebnis
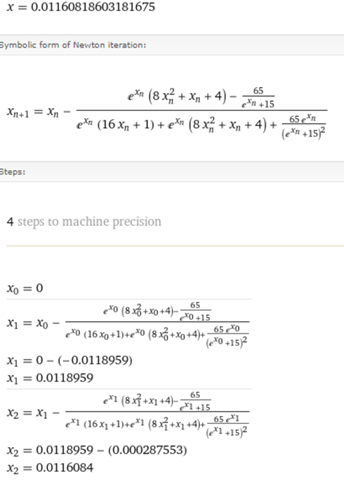
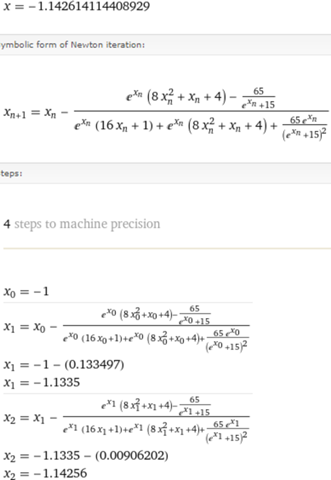
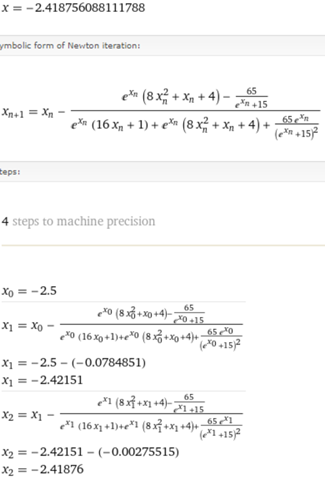


Wolfram Alpha (ein online Rechner)...
Unter Wolfram Alpha Newtonverfahren auswählen und Gleichung eingeben...

Kannst du mal zeigen wie du die gleichung aufgeschrieben hast, bei mir steht immer nur "not a valid input"

Das Newtonverfahren löst die Nullstellen einer Funktion.
Deine Gleichung ist aber noch nicht nach 0 umgestellt, also geht es noch nicht:
e^x * (8x² + x + 4) = 65 / (15 + e^x) | -(65 / (15 + e^x))
e^x * (8x² + x + 4) - 65 / (15 + e^x) = 0
Du musst also "e^x * (8x² + x + 4) - 65 / (15 + e^x)" eingeben (und einen beliebigen Startwert).

cool danke hat geklappt. Danke für deine Hilfe.

Das dürfte nur numerisch gehen, da die Kombination von Polynom und Exponentialfunktion keine geeignete Substitution zuläßt.
https://www.arndt-bruenner.de/mathe/scripts/gleichungssysteme2.htm
kommt auf x = 0,011608186058633318
als Lösung. Beachte bitte für die Exponentialfunktion nicht e^x, sondern exp(x) zu verwenden, sonst wird e als zusätzliche Variable betrachtet :-).

Dankeschön. Kennst fu vielleicht einen Weg wie ich es schaffe es schriftlich zu machen. Ich brauche das nämlich für meine mündliche Prüfung?

Ich werde dir das bestimmt nicht aufschreiben. Du musst die Gleichung in Nullstellenform umwandeln und dann darauf ein geeignetes Verfahren, zum Beispiel das
https://de.m.wikipedia.org/wiki/Newtonverfahren
anwenden. In einer mündlichen Prüfung wirst du allerdings höchstens gefragt wie das Newtonverfahren dazu aussieht, nicht wie eine konkrete Berechnung aussieht.

Im Allgemeinen lassen sich derartige Kombinationen aus Polynomen und Exponentialfunktionen nicht "elementar" (darstellbar durch "elementare Funktionen") lösen.
Wenn man die Lambertsche W-Funktion ebenfalls als elementar bezeichnet, kann man ein paar mehr solche Gleichungen elementar lösen. Aber natürlich immer noch nicht alle.
Auf Anhieb sehe ich hier keine Möglichkeit, die Gleichung so umzuformen, dass sie auf diese Weise lösbar ist. (Das heißt nicht, dass es keine gibt.)
Für numerische Lösungen gibt es mehrere Verfahren - das ist eine Wissenschaft für sich.

Du berechnet x und setzt es dann in eine der beiden Gleichungen ein um y zu erhalten. Dann hast du die beiden Koordinaten des Schnittpunkts.


Kannst mir sagen, wie du das gemacht hast?