Wie geht diese Aufgabe in der Mathearbeit?
Hallo,
Ich hatte eine Mathearbeit (10.Klasse) über Trigonometrie und Strahlensätze. War ziemlich einfach bis auf eine Aufgabe.
Die ging ungefähr so:
Ein Kanal hat die Form eines gleichschenkliges Trapez im Querschnitt. Die Sohle hat eine Länge von 5,40m. Der Böschungswinkel ist 34,8⁰.
a) Wie lautet die Breite an der Wasseroberfläche wenn der Wasserspiegel um 2,58m steigt?
b) Wie viel Wasser passt im Kanal bei einer Länge von 0,7km.
Ich versteh nicht wirklich wie man das ausrechnen muss. Der Rest war jedoch einfach.
Mfg
3 Antworten
a)
Teil den Kanal in der Mitte durch. Dann hast du zwei rechtwinklige Dreiecke, eines endet im Kanalboden, das andere an der Wasseroberfläche. Wenn du diese Seitenlängen dann verdoppelst, kannst du die Breite an der Wasseroberfläche ausrechnen.
b)
Das Volumen berechnet sich aus Querschnittsfläche mal Länge. Die Länge ist gegeben, mit dem Winkel und den beiden Seitenlängen aus a) solltest du auf die Fläche des Trapezes kommen.
Du musst die Seiten des Kanals und die Symmetrieachse verlängern, dann bekommst du Dreiecke.
| - - - - - - / <- Wasseroberfläche
| ........./
| - - - / <- Kanalboden
|..../
|/
Skizze machen!
Eine Seite betrachten. Vom Endpunkt der Sohle nach oben Höhe h eintragen (vermutlich 2,58m, "steigt" könnte aber auch bedeuten, dass eine Ausgangshöhe angegeben war).
tan alpha = x/h (was ist in diesem Zusammenhang der Böschungswinkel? Skizze bei der Aufgabe?)
Breite der Wasseroberfläche ist 2x + 5,4 m.
Bei b Formel für Trapezfläche nutzen und mal 700 m nehmen.
Guggst du
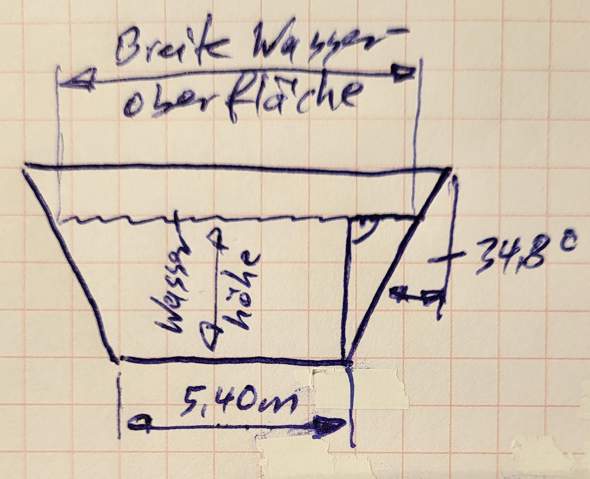
Skizze hilft!
Immer!
Siehst du das rechtwinklige Dreieck? Na dann los!
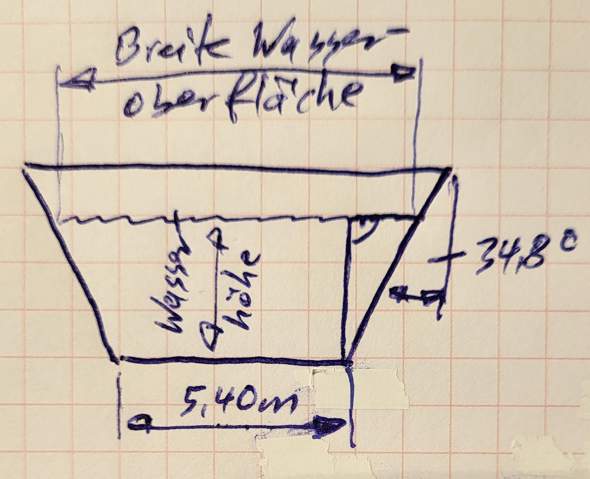
Ich verstehe das immer noch nicht 😭 b) hab ich verstanden, aber bei a) hat man doch keine rechtwinklig dreiecke oder ??