Gleichschenkliges Trapez konstruieren mit Zirkel?
Hallo ich kapiere Mathe nicht. Kann mir wer erklären wie man ein Gleichschänkkiches Dreieck konstruiert wenn keine Winkel Angegeben sind? Aufgabe: a=5cm c=4cm d=4,5cm
3 Antworten
zum Ersten: Trapez != Dreieck
zur Konstruktion:
- eine Seite malen.
- Einen Zirkel auf die Länge einer der verliebenen Seiten einstellen
- in eine der Endpunkte der bereits gemalten Seite einstechen und Kreis zeichnen
- Zirkel auf die Länge der verliebenen Seite einstellen
- in den unbenutzen Endpunkt einstechen, Kreis zeichnen
- die Schnittpunkte der beiden Kreise (WENN sie denn existieren!!) sagen dir, wo die Ecke zwischen den beiden noch ungezeichneten Seiten liegen muss. JA es gibt zwei Lösungen und du darfst dir eine aussuchen!
- Es kann sein, dass es keine Schnittpunkte gibt: Aufgabe nicht lösbar, da die Dreiecksungleichung nicht erfüllt ist!
Hinweis: es ist aus Platzgründen oft ratsam a) mit der längsten Seite zu beginnen und diese möglichst horizontal zu zeichnen b) die zu bestimende Ecke oberhalb der gezeichneten, ersten Seite zu wählen.
Ja ich habe jetzt 2 Schnittpunkte und weiß nicht weiter
Du wählst einen der Schnittpunkte aus. Dann malst du von dem gewählten Schnittpunkt eine Gerade zu jedem der beiden Kreismittelpunkte. Das ergibt ein Dreiekc mit den von dir gesuchten Seiten :)
Und gib mir den "Daumen Hoch", sonst fühle ich mich nicht gewürdigt. Das ist wichtiger als "Danke" zu sagen.
Das ist Geometrie, nicht Mathe.
Ein Dreieck braucht immer nur drei Bedingungen, um konstruiert zu werden. Du hast 4 Bedingungen. Daher geht das schon einmal nicht. Streiche als erstes einmal den Wert d=..., denn ein Mass d gibt es sowieso nicht im gleichschenkligen Dreieck.
Demzufolge gibt es den Wert von a oder c zwei Mal. Nach der klassischen Bezeichnung wird die strecke a und b gleich lang, die strecke c wird zur dritten Seite.
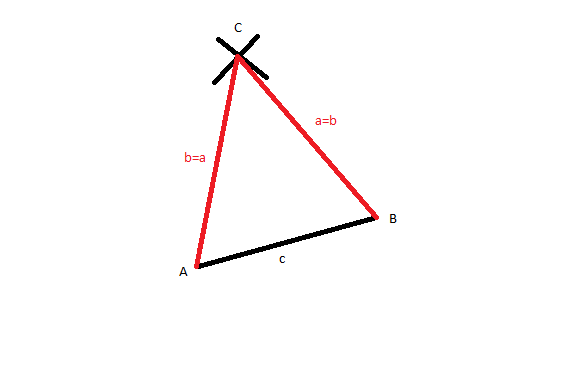
Zeichne also erst die strecke c. Dann mit dem Zirkel von den Enden der strecke c jeweils auf die gleiche Seite das Mass a abtragen. In einem der Schnittpunkte liegt C. Verbinde C mit A und B.
Was denn jetzt? Trapez oder Dreieck???
Zum Trapez siehe meinen Kommentar zu meiner Antwort auf Deine gleiche Frage unter
Dreiecksungleichung: die Summe der Längen zweier beliebiger Seiten eines Dreiecks ist immer größer als die Länge der verbliebenen Seite.