Wann Folgepfeil und wann Äquivalenzpfeil benutzen?tan⁡(α)=x⟹arctan⁡(x)=α?

Hallo,

mir ist klar, dass man bei Termumformungen Äquivalenzpfeile setzt ausgenommen beim Quadrieren und Wurzel ziehen. Aber wie sieht es aus, wenn man von tan⁡(α)=x zu arctan⁡(x)=α umformen möchte? Setzt man da auch ein Äquivalenzpfeil oder nur ein Folgepfeil, wie im Titel? Am besten mit einer Begründung also nicht nur abstimmen, Danke! :)

Ich hoffe Ihr könnt mir helfen!

Answer 1

[Willy1729]

Hallo,

folgt aus arc (45°)=1, daß der Arkustangens von 1 auch 45° ist?

Ja und nein. Natürlich gehört zu einem Tangens von 1 ein Winkel von 45°.

Aber auch der Winkel 225° (180°+45°) hat einen Tangens von 1.

Auch der Tangens von 405° ist 1. Allgemein: tan (45°+k*180°) mit k Element der ganzen Zahlen ist gleich 1.

Du kannst also aus tan (a)=1 nicht automatisch schließen, für welchen Winkel genau a steht. a=45° ist nur eine von unendlich vielen Möglichkeiten.

Wenn Du allerdings den Definitionsbereich für a auf das Intervall ]-90°;90[ einschränkst, ist die Zuordnung von Tangens und Winkel eineindeutig und Du kannst sogar den Äquivalenzpfeil benutzen.

Wenn Du die Ränder -90° und 90° aus dem Definitionsbereich herausnimmst, hast Du auch keine Probleme mit den nichtdefinierten Tangenswerten für diese Winkel, die gegen minus bzw. plus unendlich gehen.

Herzliche Grüße,

Willy

Answer 2

[mihisu]

Keine der beiden Abstimmungsmöglichkeiten ist allgemein richtig.

Beispielsweise ist für α = π und x = 0 ...

$\tan\left(\alpha\right)=\tan\left(\pi\right)=0=x$

..., aber ...

$\arctan\left(x\right)=\arctan\left(0\right)=0\ne\pi=\alpha$

Demnach ist in diesem Fall dann tan(α) = x eine wahre Aussage und arctan(x) = α eine falsche Aussage. Damit handelt es sich in diesem Fall bei ...

$\tan\left(\alpha\right)=x\ \ \Leftrightarrow\ \ \arctan\left(x\right)=\alpha$

... und ...

$\tan\left(\alpha\right)=x\ \ \Rightarrow\ \ \arctan\left(x\right)=\alpha$

... jeweils um eine falsche Aussage. Denn ...

============

Allgemein richtig wäre hingegen:

$\tan\left(\alpha\right)=x\ \ \Leftarrow\ \ \arctan\left(x\right)=\alpha$

... bzw. ...

$\arctan\left(x\right)=\alpha\ \ \Rightarrow\ \ \tan\left(\alpha\right)=x$

============

Wenn man hingegen zusätzlich fordert, dass -π/2 < α < π/2 bzw. -90° < α < 90° ist, sind unter Berücksichtigung dieser Einschränkung tatsächlich auch ...

$\tan\left(\alpha\right)=x\ \ \Leftrightarrow\ \ \arctan\left(x\right)=\alpha$

... und ...

$\tan\left(\alpha\right)=x\ \ \Rightarrow\ \ \arctan\left(x\right)=\alpha$

... wahr.

============

Ein Äquivalenzpfeil (⇔) ist dann richtig, wenn die beiden damit verbundenen Aussagen äquivalent sind. Also wenn die eine Aussage genau dann wahr ist, wenn auch die andere Aussage falsch ist.

Ein Folgepfeil (⇒)[von links nach rechts] ist dann richtig, wenn gilt: Ist die linke Aussage wahr, so muss auch die rechte Aussage wahr sein. (Allerdings kann die rechte Aussage durchaus auch dann wahr sein, wenn die linke Aussage falsch ist.)

Comments

[mihisu]

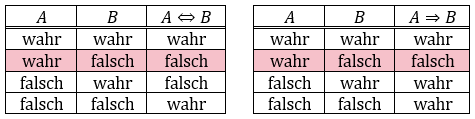
Uups, kleiner Schreibfehler.

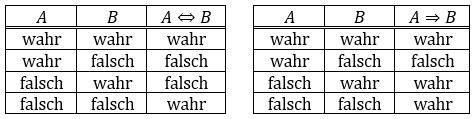
Ein Äquivalenzpfeil (⇔) ist dann richtig, wenn die beiden damit verbundenen Aussagen äquivalent sind. Also wenn die eine Aussage genau dann wahr ist, wenn auch die andere Aussage falsch ist.

... sollte eigentlich lauten ...

Ein Äquivalenzpfeil (⇔) ist dann richtig, wenn die beiden damit verbundenen Aussagen äquivalent sind. Also wenn die eine Aussage genau dann wahr ist, wenn auch die andere Aussage wahr ist.

[Bzw. könnte man auch sagen: „Also wenn die eine Aussage genau dann falsch ist, wenn die andere Aussage falsch ist.“]

Answer 3

[ralphdieter]

Wie mihisu schon ausgeführt hat, gilt generell nur:

✔ mit Folgt-aus-Pfeil: tan⁡(α)=x ⇐ arctan⁡(x)=α

Bei Termumformungen verwendet man übrigens das Gleichzeichen. Von Äquivalenz redet man beim Umformen von Gleichungen und anderen Aussageformen.

Zwei Gleichungen sind äquivalent, wenn sie für jede Belegung der Variablen entweder beide wahr oder beide falsch sind. Suchst Du alle Belegungen, die eine Gleichung erfüllen, sind Äquivalenzumformungen natürlich sehr praktisch.

Manchmal kommt man so aber nicht zum Ziel. Dann macht man gern eine Schlussfolgerung (⇒), die alle Lösungen der Ausgangsgleichung und möglicherweise noch mehr erlaubt — beim Anwenden einer nicht streng monotonen Funktion wie Quadrieren oder tan(). Am Ende muss man dann für jede gefundene Lösung prüfen, ob sie die Originalgleichung erfüllt oder nur "dazugeschlussfolgert" wurde.

Beispiel:

• x+√x=2 ⇔ √x=2-x ⇒ x=4-4x+x² ⇔ x²-5x+4=0 ⇔ x₁,₂=5/2±3/2

Bei der Probe fällt die Lösung x₁=4 durch. Nur x₂=1 passt.

Bei Umformungen, die möglicherweise weniger Lösungen haben, schreibst Du "⇐" — beim Anwenden einer auf einen Teilbereich eingeschränkten Umkehrung einer nicht streng monotonen Funktion wie Radizieren oder arctan(). Das ist okay, wenn Du nur nach irgendeiner Lösung suchst und am Ende auch eine findest. Die passt dann, aber vielleicht gibt es noch andere Lösungen. In der Praxis braucht man das eher selten.

Statt Lösungen durch "⇐" zu verlieren, schreibt man lieber alle Alternativen auf und hat damit eine Äquivalenzumformung von einer Gleichung in mehrere mögliche:

Beispiele:

• x(x-1)(x-2)=0 ⇔ x=0 ∨ x=1 ∨ x=2
• tan x=h ⇔ x=arctan h + kπ (k∈ℤ)
• x²-2x-1=0 ⇔ x₁,₂=1±√2

Comments

[ralphdieter]

Bitte ignoriere meine "Abstimmung". Ich habe nur den Text daraus kopiert. Der Haken hat sich dabei von allein gesetzt und geht einfach nicht mehr weg :-(

Answer 4

[kreisfoermig]

ran(arctan) \subseteq (-π/2, π/2).

Die ==>-Richtung stimmt gdw. a ε (-π/2, π/2).

Comments

[oesy1907]

verstehe die Begründung nicht ganz :D

[kreisfoermig]

@oesy1907

ich habe nichts begründet, nur Fakten erwähnt. Das erste ist halt so (tatsächlich mit Gleichheit) per Definition von arctan, was tan | (–π/2, π/2) invertieren soll. Jetzt beweist man dass tan | (–π/2, π/2) : (–π/2, π/2) —> (–infty, infty) injektiv ist (mithilfe der trig. Identität geht das schnell). Dann zeigt man, dass die Funktion stetig ist und deshalb, da (–π/2, π/2) topologisch zusammenhängend ist, ist das Image auch zusammenhängend und deshalb ein Interval. Da die Funktion nach oben und unten unbeschränkt ist, muss dieses Interval gleich (–infty, infty) sein. Es folgt, dass tan | (–π/2, π/2) : (–π/2, π/2) —> (–infty, infty) bijektiv ist. Darum existiert ein (eindeutiges) Inverses arctan : (–infty, infty) —> (–π/2, π/2). Insbesonder MUSS a in (–π/2, π/2) liegen.