Scheitelpunktform einer nach unten geöffnete Parabel?

Hallo,

wenn es darum geht, eine Funktion von normal- auf die Scheitelpubktform umzuwandeln, kann ich das, egal ob normal, gestreckt oder gestauchte Parabel .

Leider klappt es nicht, wenn es dich um eine nach unten geöffnete Parabel handelt, zum Beispiel:

-x²+4x+6

ich multipliziere es mit (-1) und wende dann die quadratische Ergänzung an. Es kommt bei mir folgendes:

(x-2)²-10

was mache ich falsch?

Answer 1

[SebRmR]

-x² + 4x + 6

Ich würde -1 ausklammern
-1[x² - 4x - 6]
Und jetzt vom Inhalt der [] quadratische Ergänzung
ich komme d dann auf:
-1 [(x-2)² - 10]

Und dann mit -1 Multiplizieren:
-(x - 2)² + 10

Wenn man -x² + 4x + 6 zeichnen lässt, sieht das so aus:

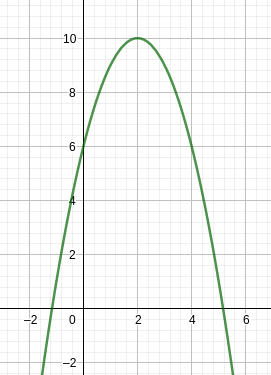
-(x - 2)² + 10 sieht so aus:

Comments

[DarkYasha]

Danke für die Erklärungen, kriege das jetzt hin :D

Answer 2

[Nayes2020]

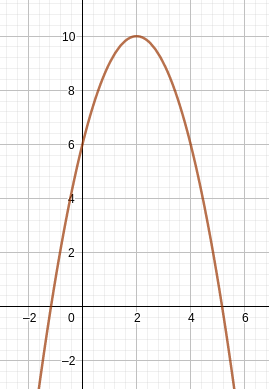
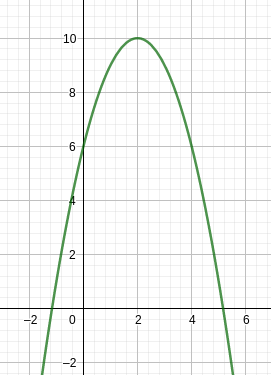
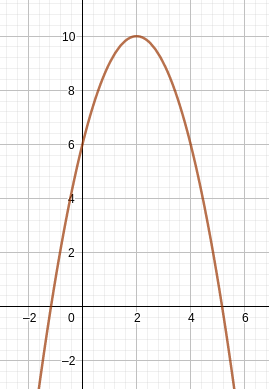
Dein b^2 ist ja 2 in Quadrat

Wenn ich das mit plus und minus Quadratisch ergänze.

Bekomme ich - (x+2)^2 +6-4

Also - (x+2)^2 +2

Woher ich das weiß: eigene Erfahrung – man lebt halt xD

Answer 3

[Rammstein53]

f(x) = -x^2 + 4x + 6

f(x) = -x^2 + 4x - 4 + 4 + 6

f(x) = - (x^2 - 4x + 4) + (4+6)

f(x) = - (x - 2)^2 + 10