Satz des Pythagoras?
Ist das richtig, dass der Umfang 29,53 cm und der Flächeninhalt 52,59 Quadratzentimeter ergibt?
Aufgabe: Die Diagonale e beträgt 9 cm und der Schenkel b 6 cm. Sie bilden in dem gleichschenkligen Trapez einen rechten Winkel.

Wenn nicht, bitte mit Begründung
1 Antwort
Ist falsch. Berechnung wie folgt.
Berechnung
a = Wurzel(b² + e²)
a = Wurzel(6^2 + 9^2)
a = 10,816654 cm
---
h = e * b / c
h = e * b / Wurzel(e² + b²)
h = (9 * 6) / Wurzel(9^2 + 6^2)
h = (9 * 6) / 10,816654
h = 54 / 10,816654
h = 4,992302 cm
---
a2 = Wurzel(b² - h²)
a2 = Wurzel(6^2 - 4,992302^2)
a2 = 3,328201 cm
-- oder --
a2 = b² / a
a2 = 6^2 / 10,816654
a2 = 3,328201 cm
---
a1 = a2
a1 = 3,328201 cm
---
c = a - a1 - a2
c = 10,816654 - 3,328201 - 3,328201
c = 4,160252 cm
---
U = a + b + c + d
U = 10,816654 + 6 + 4,160252 + 6
U = 26,976906 cm
---
A = ((a + c) / 2) * h
A = ((10,816654 + 4,160252) / 2) * 4,992302
A = 37,384619 cm²

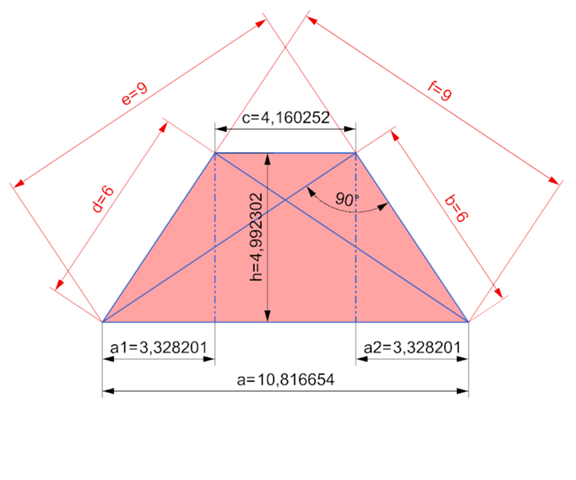
Also die 10,82 und 3,33 , die du gerechnet hast ist ok.
Die Höhe h des Trapezes hast du falsch berechnet.
h = 4,99 ist richtig. h = 6 ist falsch.
Denk noch mal darüber nach.
Beachte mein Bild. Wo das Dreieck mit 90° ist und wo h ist.
e und b ist ja gegeben. Kann man a des Trapezes berechnen.
a ist ja 10,82 cm.
Ach so, das mit h habe ich auch eben gesehen. Aber warum kann man Seite c nur mit a1 und a2 berechnen und nicht auch mithilfe von der Diagonale und der linken Seite, also 6 und 9?
Achso ja stimmt. Du kannst a1 bzw. a2 auch wie folgt rechnen.
a2 = b² / a
Ich hab auch meinen Beitrag ergänzt
Ich verstehe das irgendwie nicht, warum? Die Diagonale ist doch 9cm und es sind ja zwei, wodurch beide 9 cm sind. D beträgt auch 6 cm und dann kann man doch einfach den Satz des Pythagoras anwenden, indem man im linken Teildreieck e Quadrat minus d Quadrat rechnet, um die andere Kathete auszurechnen (oben die Seite)