Rekonstruktion von Funktionsgleichungen 4. Grades?
Ich habe Schwierigkeiten das Gleichungssystem zu lösen.Ich habe da einmal e=2,16a+4c+e=0 und 32a+4c=0 raus aber weiß jetzt nicht wie ich noch a und c rausbekomme.

4 Antworten
Ein Polynom 4. Grades sieht so aus:
f(x) = a + bx + cx^2 + dx^3 + ex^4
(Passt das zu deiner Buchstabenwahl?)
Nun weißt du, dass das Polynom symmetrisch zur Y-Achse ist. Dann tauchen nur geradzahlige Exponenten bei x auf. b = d = 0.
Der Graph geht durch (0|2), also f(0) = 2. Folglich ist a=2.
Bei x=2 hat f ein Extremum und berührt dort die X-Achse. Folglich ist dort die erste Ableitung 0 und die zweite ~=0 (sonst würde es die X-Achse schneiden, nicht berühren). Also:
f(2) = 0, f'(2) = 0
Wir waren bei: f(x) = 2 + cx^2 + ex^4
f(2) = 2 + 4c + 16e = 0 , also: c = -4e - 1/2
f'(2) = 2cx + 4ex^3 = 4c + 32e = 0, also: c = -8e
Zusammen: -8e = -4e - 1/2; -4e = -1/2; e = 1/8 und c = - 1.
Probe:
f(x) = 2 - x^2 + 1/8 * x^4

Passt.
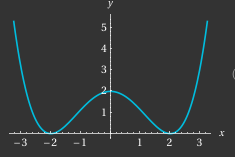
Hallo,
symmetrisch zur y-Achse bedeutet, daß die Funktionsgleichung nur gerade Potenzen von x besitzt, daher:
f(x)=ax^4+bx^2+c
f'(x)=4ax^3+2bx.
Da die y-Achse bei y=2 geschnitten wird, ist c gleich 2.
Extremstelle bei x=2 b bedeutet f')2=0. Außerdem ist bei x=2 eine Nullstelle,
also f(2)=0.
Das führt zu den Bestimmungsgleichungen für a und b:
f(2)=0:
16a+4b+2=0. Das kann man noch durch 2 teilen:
8a+2b+1=0.
f'(2)=0
32a+4b=0 und nach Division durch 4:
8a+b=0, also b=-8a.
Einsetzen in die erste Gleichung:
8a-16a+1=0.also 8a=1 und a=1/8.
Da b=-8a, ist b=-1.
Mit c=2 lautet die Gleichung daher:
f(x)=(1/8)x^4-x^2+2.
Herzliche Grüße,
Willy
16a+4c+e=0 und 32a+4c=0
e = 2 einsetzen
16a + 4c + 2 = 0
32a + 4c = 0
voneinander abziehen , damit 4c verschwindet
16a-32a + 4a-4a + 2 = 0 - 0
-16a + 0 + 2 = 0
a = -2/-16
Du hast an sich fünf Informationen:
- Den Punkt (0|2)
- Den Punkt (2|0)
- Den Punkt (-2|0) - durch Achsensymmetrie
- Die Ableitung bei x=2 ist 0, (die zweite Ableitung bei x=2 ist ≠ 0.)
- Entsprechend die Ableitungen bei x = -2
Nach dem du durch 4 geteilt hast setzt du ja wieder in eine Gleichung ein...welche meinst du denn?