pH-Wert-Änderung berechnen?

Man sollte meinen, der ausführliche Rechenweg wäre genug, aber ich habe trotzdem ein paar ganz wichtige Dinge nicht zuordnen können.
Ich berechne, soweit ich das verstehe, bei n(NH3) die Stoffmenge, die durch das HCl verbraucht wurde, also 0,05 mol. Bei n(NH4+) darunter setzte ich das einfach mit diesem Wert gleich, denn wenn soviel mol NH3 verbraucht wurden, müssen in der Lösung auch soviel NH4+-Teilchen sein. Ich habe nur nicht ganz verstanden, welche Werte es sind, die ich in die Hasselbalch-Gleichung einsetzen soll, da in der Aufgabe ja alles 0,05 mol sind. Die nBase könnten ja die 0,05 mol sein, die noch übrig sind, oder die die verbraucht wurden. Und die nSäure könnten die 0,05 mol HCl sein, die zugesetzt wurden, oder die 0,05 mol NH4+, die sich gebildet haben. Soweit ich weiß, ist der Wert ja meistens gleich, weil sich ja soviel NH4+ bildet, wie auch Säure hinzugesetzt wird. Aber sicher bin ich mir nicht. Und bei nBase bin ich mir wie gesagt auch nicht sicher.
In einer anderen Aufgabe sind es beispielsweise 0,7mol CH3COOH (pKs=4,75). Diesen wird 0,1 mol NaOH zugesetzt. Ich habe pH(nach Basenzugabe)=4,75+lg(0,1mol/0,6mol)=3,97 gerechnet. Die 0,6 mol habe ich so gerechnet: 0,7 (Säurestoffmenge) - 0,1 (Basenstoffmenge). Macht das Sinn oder muss ich andere Werte einsetzen?
Entschuldigung für die vielen Fragen.
2 Antworten
Hi,
In deinem Ammoniak-Ammonium-Puffer liegt NH3 als Base und NH4(+) als konjugierte Säure vor. Die 0,05 Mol sind jeweils das, was nach der Säurezugabe vorhanden ist (dann ist nämlich erst der Puffer ausgebildet).
Zur zweiten Reaktion: CH3COOH + NaOH --> CH3COONa + H2O
Essigsäure ist eine mittelstarke Säure, man rechnet wie bei schwachen Säuren. Es gilt also vor der Reaktion pH = 0,5(pKs - lg cS) = 0,5(4,75 - lg(0,7)) = 2,45.
Nach der Säurezugabe wurden die 0,1 Mol Säure verbraucht, die Stoffmenge der Säure ist also, wie du richtig schreibst, 0,6 Mol. An Acetat entsteht nur 0,1 Mol. Denn die 0,1 Mol, die an Säure abreagieren, reagieren zum Acetat. Es gilt also nach Henderson-Hasselbalch:
pH = pKs + lg(0,1/0,6) = 3,97.
Du hast also komplett richtig gerechnet.
LG
Die Konzentrationen in der Henderson–Hasselbalch-Gleichung sollten eigentlich die Gleichgewichtskonzentrationen sein (in diesem Fall ist die Gleichung keine Näherung, sondern korrekt im Rahmen der üblichen Idealisierungen, i.e., Konzentrationen statt Aktivitäten etc.). Meist kennt man die Gleichgewichtskonzentrationen aber nicht und verwendet dann die Einwaagekonzentrationen (oder formalen Konzentrationen); dann ist HH nur eine Näherung, aber sie funktioniert gut, solange die Puffersubstanzen wesentlich höher konzentriert sind als H₃O⁺ und OH¯.
Eine c=0.1 mol/l (pKb =4.75) hat pH=11.12; Deine Näherungsformel liefert 11.13, was fapp dasselbe ist, der winzige Unterschied entsteht daraus, daß auch diese Formel streng genommen nur korrekt ist, wenn man die NH₃-Gleichgewichtskonzentration einsetzt. Da real 1.3% des Ammoniak gemäß
NH₃ + H₂O ⟶ NH₄⁺ + OH¯
wegreagiert hat, ist die Gleichgewichtskonzentration c(NH₃)=0.0987 mol/l. Weil Ammoniak nur eine schwache Base ist, bleibt der Fehler unbedeutend klein; in schwierigeren Fällen kann man eine stärkere Formel verwenden, nämlich
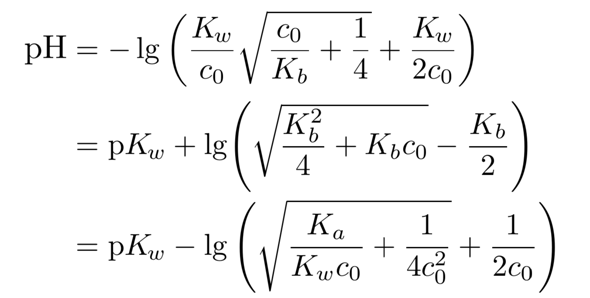
die diesen Effekt handhaben kann, aber immer noch eine Näherung beinhaltet, nämlich daß alle OH¯-Ionen aus dem Ammoniak kommen (die aus der Autoprotolyse werden ignoriert).
Wenn Du jetzt zu dieser Suppe 0.05 mol HCl zugibst, dann reagiert die mit genau der Hälfte des NH₃ zu NH₄⁺. Du kriegst also einen symmetrischen Puffer, und die HH-Gleichung sagt in diesem Fall pH=pKa=pKw−pKb voraus. In diesem Fall ist die Näherung sehr gut; wir haben die Puffersubstanzen in Konzentrationen 0.05 mol/l, und aus pH=9.25 folgt ja c(OH¯)=0.00002 mol/l, also viel kleiner (die Gleichgewichtskonzentrationen für NH₃ und NH₄⁺ sind offenbar c₀±c(OH¯), also 0.04998 bzw. 0.05002 mol/l, das ist weniger als 1‰ Abweichung).
TL; DR: In die üblichen Näherungsformeln setzt man die formalen Konzentrationen ein und hofft, daß die Gleichgewichtskonzentrationen davon nicht weit abweichen. Wer vorsichtig ist, überprüft das nachher vom Ergebnis her noch einmal zurück.
Stellt sich noch die Frage, was ist, wenn man die Näherungen nicht mehr verwenden kann, weil der Puffer entweder stark verdünnt ist oder einen pH nahe an den Grenzen des pH-Bereichs hat? Ein Beispiel wäre eine Mischung aus Hydrogensulfat und Sulfat (pKₐ=1.99), jeweils 0.05 mol/l. Der pH ist 2.12 und nicht wie mit HH berechnet 1.99. Die dabei anzuwendende Formel lautet
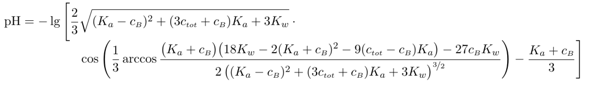
und vermutlich siehst Du auf den ersten Blick, warum niemand damit rechnen will. Dabei ist ctot die Gesamteinwaagenmenge Sulfat (summiert über die saure Form HSO₄¯ und die basische SO₄²¯), und cB ist die Konzentration der basischen Form, also SO₄²¯. Diese Formel ist so konstruiert, daß sie mit den Einwaagekonzentrationen richtig ist; außerdem ist sie extrem allgemein, Du darfst damit jede Menge Blödsinn treiben, z.B. cB=0 (dann rechnest Du reine Säure aus) oder sogar cB<0 (das würde einer Mischung aus einer beliebigen Säure mit Säurekonstante Kₐ und Konzentration ctot plus |cB| einer starken Säure wie HCl bedeuten); Du kannst sogar ctot=0 setzen, und je nachdem, ob cB größer oder kleiner als Null ist, rechnest Du dann den pH einer starken Base oder Säure aus (mit korrekter Beschränkung auf pH→7 im Falle sehr hoher Verdünnung). Mit dieser Formel kann man ziemlich viel Spaß haben. ☺
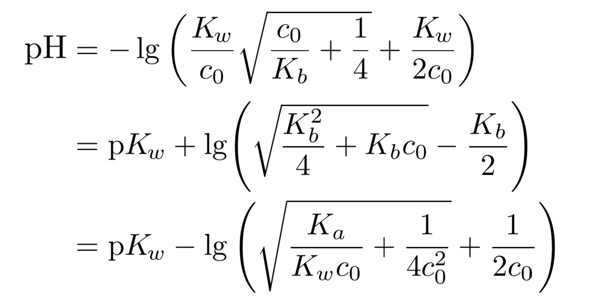
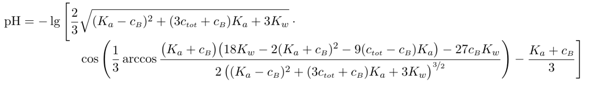
Okay dann weiß ich Bescheid, danke!