Mathematik - IQ?
Guten Tag.
Ich würde gerne um Ihre Hilfe bitten - können Sie mir bitte bei folgender Aufgabe helfen? Was ist mit den Sigma-Regeln gemeint bzw. was muss ich berechnen?
Die Verteilung des Intelligenzquotienten in der Bevölkerung ist normalverteilt mit 𝜇 = 100
und 𝜎 = 15.
a) Berechne, mit welcher Wahrscheinlichkeit eine zufällig ausgewählte Person
hochbegabt ist (also einen IQ von mindestens 130 besitzt) (zunächst mit Sigma-Regeln, dann mit GTR).
- mit dem GTR kriege ich übrigens ein Ergebnis von 0,973402 heraus
Danke.
2 Antworten
Es gibt so Standard-Integralwerte unter einer normierten Gaussglocke. Ich glaube, das sind bei +/- 1 sigma 68 %, bei +/- 2 sigma 95 % etc. Diese Werte kann man relativ schnell im Rahmen einer Google-Bildersuche finden.
Ich habe mir auch mal ein kleines Matlab-Skript geschrieben:
IQ = 130;
mu = 100;
sigma = 15;
glocke = @(x) (1/(sqrt(sigma^2*2*pi)))*exp(-(x-mu).^2/(2*sigma^2));
Prozentrang = 1-integral(glocke,IQ,Inf)
Haeufigkeit = integral(glocke,IQ,Inf)
Vielleicht entspricht dein Ergebnis eher dem Prozentrang? Anhand des Skripts siehst du, dass der Prozentrang das Integral von 130 abwärts darstellt, während die Formulierung "mindestens 130" das Integral in die andere Richtung beschreibt. Da das Integral der Normalverteilung mit 1 definiert ist, musst du dein Ergebnis also einfach von 1 abziehen. Das haut auch zahlenmäßig ungefähr hin (nicht ganz genau, aber schließlich arbeitest du auch mit einem GTR)
Wenn man einen IQ-Test entwickelt, testet man ihn an mehreren 1000 oder 10.000 Menschen. Die Ergebnisverteilung des Tests ergibt näherungsweise eine Gaußsche Glocke. Dementsprechend gibt der IQ an, wie ein Einzelner auf dieser Glocke liegt. Da es unterschiedliche Tests gibt und die Anzahl der richtig beantworteten Fragen nicht immer übereinstimmen, normiert man die Tests auf den IQ. So kann man bei jedem Test sagen "der Durchschnitt ist 100 +/- 15" unabhängig davon, ob der Durchschnitt 20 von 100 Fragen richtig beantwortet und um 5 Antworten streut oder 60 von 100 +/- 20 Fragen richtig beantwortet wurden.
Jetzt habe ich es, danke! Mir fehlte die Erklärung, dass ich den Wert nochmal durch 2 teilen muss.
Danke. Die drei Sigma-Regeln kenne ich auch, allerdings verstehe ich nicht, welche bzw. wie ich die hier anwenden soll? Ich soll doch ermitteln, wie hoch die Wahrscheinlichkeit ist, dass eine zufällige Person hochbegabt ist. Was soll ich dann mit den Sigma-Regeln machen?
Hochbegabung definiert sich dadurch, dass jemand mit seinem IQ mindestens zwei Standardabweichungen (2 sigma) vom Erwartungswert nach oben abweicht. Also 130 bei sigma = 15 und µ = 100. µ + 2 sigma = 130.
Da die Standardabweichungen bei der Normalverteilung symmetrisch um den Erwartungswert liegen und die 2 sigma ein Integral von ca. 0,95 einschließen, musst du das Äußere (1-0,95) nochmal halbieren, um nur die obere Hälfte des Äußeren (130 bis unendlich) zu ermitteln.
Hier arbeitet man mit der kumulierten Normalverteilung.
https://onlinestatbook.com/2/calculators/normal_dist.html
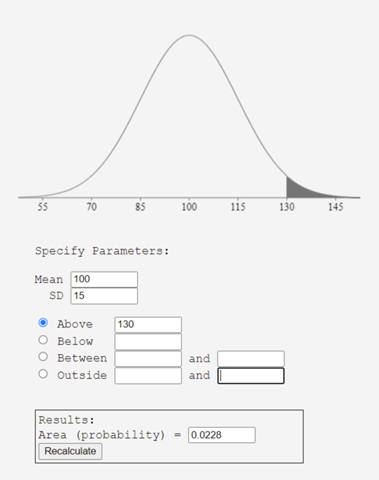
Die gesuchte Wahrscheinlichkeit beträgt somit 2,28%.
mit dem GTR kriege ich übrigens ein Ergebnis von 0,973402 heraus
Das ist die Wahrscheinlichkeit, dass jemand einen IQ unter 130 hat.
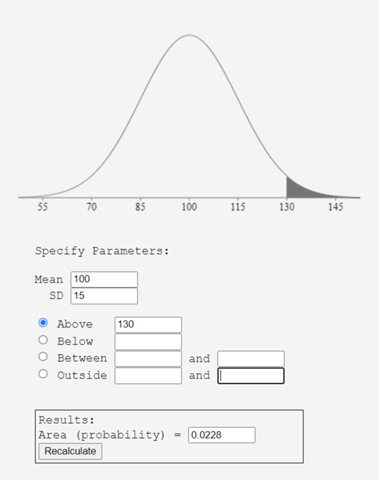
Das stimmt. Ich merke gerrade, dass die 0,97340 für das Intervall bis 129 gelten; das müsste ich noch von 1 abziehen. Aber was bringen mir die Sigma-Regeln hier?