Kann mir hier jemand helfen?

Also bei dieser Aufgabe 2 mit Bezug zu den linearen Funktionen.

Answer 1

[gauss58]

(1) s_1 = v_1 * t_1

(2) s_2 = s - s_1 = v_2 * t_2 = v_2 * t_1

(1) in (2) führt zu:

s - v_1 * t_1 = v_2 * t_1

t_1 = s / (v_1 + v_2)

t_1 = 30 km / (8 km/h + 16 km/h)

t_1 = 1,25 h

Comments

[User81011801]

@gauss58 Also dann das hier für den Treffpunkt oder?
s1 =v1 ⋅t1 =8km/h⋅1,25h=10km

t2 =t1 =1,25h

s2 =v2 ⋅t2 =16km/h⋅1,25h=20km

[gauss58]

@User81011801

ja richtig

[User81011801]

@gauss58

danke für alles Kollege, wünsche dir noch einen schönen Abend

[User81011801]

@gauss58

Noch eine Frage. Hätte man auch andere Werte also beispielsweise 7km/h und 14km/h verwenden können oder wie genau bist du auf 8km/h und 16km/h gekommen? Entschuldigung wenn es eine dumme Frage ist, aber das müsste ja eigentlich auch gehen, solange die Beziehungen gleich sind.

[User81011801]

@User81011801

Oder @evtldocha kannst du das mir vielleicht sagen?

[gauss58]

@User81011801

Hans Dampf fährt 12 km in 1,5 h. Das sind in einer Stunde 12 km/1,5 h = 8 km/h. Und das Schiff fährt 16 km/h.

Mit 7 km/h und 14 km/h käme ein größerer Wert für die Zeit heraus, aber mit den kleineren Geschwindigkeiten multipliziert, kämen auch 10 km und 20 km heraus. Entscheidend ist hier das Verhältnis der Geschwindigkeiten zueinander.

Answer 2

[GreenxPiece]

Wenn beide zur gleichen Zeit ablegen und schiff 2 doppelt so schnell fährt, treffen sie sich 10km von der Insel entfernt. Schiff 1 fährt so 10 km in Zeit t und Schiff 2 fährt den doppelten weg also 20 km in Zeit t. Ergibt zusammen 30 km.

Um die Zeit t zu bekommen reicht ein einfacher dreisatz.

Schiff 1 fährt 12 km in 90 minuten

Also fährt es 1km in 90/12 Minuten = 7,5 minuten

Und 10 km in 7,5*10 Minuten = 75 minuten

Also treffen sie sich 1 Stunde und 15 Minuten nach Start.

Answer 3

[verreisterNutzer]

Wenn v_HD die Geschwindigkeit des Schiffes von Hans Dampf ist dann haben wir 2 lineare Gleichungen (der Ursprung des Koordinatensystems befinde sich am Abfahrtspunkt von Hans Dampf)

$\left(1\right)\ s_{HD}\left(t\right)\ =\ v_{HD}\cdot t$ $\left(2\right)\ s_{eS}\left(t\right)\ =30\ km\ -\ v_{eS}\cdot t\ =30\ km\ -\ 2\cdot v_{HD}\cdot t$

(Der Index HD steht für Hans Dampf und der Index eS für entgegenkommendes Schiff)

Durch Gleichsetzen der Gleichungen (1) und (2) findest Du die Zeit bis zum Aufeinandertreffen der beiden Schiffe. Dabei ergibt sich:

$3\cdot v_{HD}\cdot t\ =\ 30\ km\ \ \ \ \ \ \ \ \ |\ \ :\ \left(3\cdot v_{HD}\right)$ $t=\frac{30\ km}{3\cdot\ v_{HD}}=\frac{10\ km}{v_{HD}}$

Fehlt also noch der Wert die Geschwindigkeit v_HD des Schiffes von Hans Dampf. Die ist im Text gegen mit

$v_{HD}=\frac{12\ km}{1.5\ h}=\frac{12}{\frac{3}{2}}\frac{km}{h}=\frac{24}{3}\frac{km}{h}=8\ \frac{km}{h}$

Damit ist dann:

$t=\frac{10\ km}{8\ \frac{km}{h}}=1,25\ h\ \ \ \left(1\ Stunde\ und\ 15\ Minuten\right)$

Die beiden treffen sich bei Kilometer

$s_{HD}\left(1,25\ h\right)\ =8\frac{km}{h}\cdot1,25\ h\ =\ 10\ km$

(vom Abfahrtspunkt von Hans Dampf aus gemessen)

Skizze:

Comments

[User81011801]

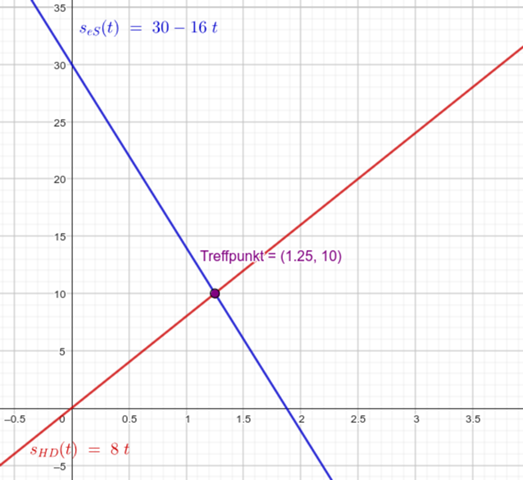
Kannst du mir auf meine Frage unter gauss58 eine Antwort bitte geben?

Answer 4

[Clemens1973]

Du kannst Gleichungen aufstellen für die zurückgelegten Wege s1(t) von Hans Dampf und s2(t) des entgegenkommenden Schiffes. Mit v=12/1.5km/h und s0=30km gilt

$s_1(t)=v\cdot t$

$s_2(t)=s_0-2\cdot v\cdot t$

Nun gleichsetzen s1(t)=s2(t) und nach t auflösen. Über die Funktion s1(t) folgt dann der Abstand von der Insel.