Ist die Funktion x^x hier definiert?
Es herrscht scheinbar Uneinigkeit über den Definitionsbereich von x^x. Einige sagen, die Funktion sei nur für x > 0 definiert. Hierbei wird argumentiert, dass wir das Problem der Wurzel aus negativen Zahlen hier hätten , welche im Bereich der reelen Zahlen nicht existieren.
Allerdings erhalten wir einerseits bei ganzzahligen negativen Werten ja reele Zahlen als Ergebnis. Als Beispiel:
Andererseits hätten wir auch noch die rationalen negativen Zahlen, die als Bruch geschrieben einen ungeraden Nenner haben bzw. als Dezimalzahl geschrieben die letzte Nachkommastelle ungerade ist.
Mit der Annahme, kommen wir zu meiner eigentlichen Frage. Wir hätten ja jetzt nun genauso viele definierte wie undefinierte Werte bei negativen x-Werten, da sich gerade und ungerade Zahlen stets abwechseln.
Wäre f(x), wobei x gegen -0 läuft, nun definiert oder nicht?
5 Antworten
Ein ganzzahliger Exponent ist auch bei einer negativen Basis problemlos. Bei rationalen Exponenten hast Du richtig erkannt, dass ein gerader Nenner Probleme macht.
Für ungerade Nenner könntest Du das Vorzeichen am Zähler (gerade/ungerade) festmachen – nur so lassen sich die Rechenregeln für Potenzen noch einigermaßen retten.
Dann hast Du (−1)ʳ für „halb ℚ“ definiert. Der Graph schaut aus wie y=±1, wobei oben alle Werte für Brüche der Form „g/u“ und unten alle für „u/u“ liegen. Die Stetigkeit kannste in die Tonne treten, und eine Erweiterung auf ℚ oder ℝ wäre bestenfalls willkürlich.
Fazit: Wenn Du den Definitionsbereich von f(x)=xˣ auf „g/u“ einschränkst, ist f stetig. Bei „u/u“ hat sie in 0 eine Sprungstelle, und wenn Du beides zulassen willst, ist sie überall auf (−∞, 0] unstetig.
Es kann natürlich sein, dass so eine Definition für einen bestimmten Anwendungsfall ganz praktisch ist, aber im Allgemeinen lassen Mathematiker das im Reellen lieber undefiniert. Denn im Komplexen bietet sich eine wesentlich schönere Definition an, die der von oben widerspricht.
"Definitionsbereich von x^x. Einige sagen, die Funktion sei nur für x > 0 definiert. "
Na, das ist halt schlicht und einfach unsinnig, denn x^x ist auch für gewisse negative x-Werte (nämlich die ganzzahligen) ganz klar und einfach und eindeutig definierbar. Für gewisse Zwecke ist es aber sinnvoll, den Definitionsbereich einzuschränken, was dann aber keine "grundsätzliche" Nicht-Definierbarkeit bedeutet !
Ferner:
Etwa einem Ausdruck wie (-1/3) ^ (-1/3) einen Wert zuzuordnen, halte ich für eher problematisch und in den allermeisten "vernünftigen" Situationen auch für sinnlos. Genau mit derartigen verkorksten Definitionen ist man dann meistens schon ganz nahe an "Teufels Küche" - insbesondere wenn man dann noch versucht, sowas wie "allgemeine Regeln" aufzustellen. Wie vergleicht man dann etwa die Werte von (-1/3) ^ (-1/3) und (-2/6) ^ (-2/6) ? ......
Es herrscht scheinbar Uneinigkeit über den Definitionsbereich von x^x. Einige sagen, die Funktion sei nur für x > 0 definiert.
... wo herrscht diese Uneinigkeit?
Es gilt
und damit sollte wegen ln(x) klar sein, dass die Funktion nur für x>0 definiert ist. Da kannst Du Dir jede weitere Rechnerei mit Beispielen sparen.
"Es gilt
und damit sollte wegen ln(x) klar sein, dass die Funktion nur für x>0 definiert ist."
Da muss ich recht vehement protestieren ! Um zu dieser Umformung von x^x zu (e^(ln(x)))^x zu kommen, muss man schon voraussetzen, dass x positiv ist.
Es gibt aber auch noch etwa die negativen ganzen Zahlen, für welche die Potenz x^x sehr wohl definiert ist, nur der Logarithmus nicht !
Ich habe die Antwort kommentiert. Sie ist zwar unterm Strich richtig, aber die Begründung ist etwas schwach.
Ok - da hast Du recht, das Argument ist nicht gut. Dann muss wohl eher herhalten, was ich mit (-1/2)^(-1/2) anfangen sollte ohne mit den Potenzgesetzen und Wurzelgesetzen einen Konflikt heraufzubeschwören.
Die Uneinigkeit habe ich auf anderen Fora herauslesen können.
Offenbar kommen ja dennoch, wie in den Rechnungen gezeigt, reelle Zahlen als Ergebnis heraus. In Desmos werden mir jene Funktionswerte ebenfalls angezeigt. Wenn ich die Funktion -x^-x plotte, dann wird mir für positive x-Werte eine stetige Kurve ausgegeben, trotz der Tatsache, dass man -x^-x als e^[-x * ln(-x)] umschreiben kann.
Offenbar kommen ja dennoch, wie in den Rechnungen gezeigt, reelle Zahlen als Ergebnis heraus
Nein, kommen nicht raus, da man nicht rechnen kann, was nicht definiert ist. Der Logarithmus negativer reeller Zahlen ist nicht definiert und damit ist alles, was Du an Rechnungen mit negativen x-Werten hinschreibst undefiniert. Mehr ist dazu mathematisch nicht zu sagen.
Wenn ich die Funktion -x^-x plotte
Das ist aber was anderes als (-x)^(-x)
Okay gut, macht Sinn. Wenn wir dennoch eine Funktion hätten, die so aussähe wie dieser Graph, also die im Negativen periodisch definiert und undefinierte Funktionswerte aufweißt, wäre dann der nächste Wert unter 0 definiert oder undefiniert? Oder kann man das nicht sagen?
während (-8)^-8 voll normal ist
ist doch bei (-8.1)^-8.1 sofort i im Spiel
deine Idee hatte ich auch schon , aber ich kenne keine Fkt die nur aus Punkten besteht
Generell haben exponentialfunktionen immer eine positive Basis, weil die Funktion sonst hoch und runter gehen würde.
für zum Beispiel (-1/2)^(-1/2) gibt es auch keine Lösung, weil unter der Quadratwurzel keine negative Zahl stehen darf, deine Rechnungen oben haben auch ein paar Fehler, z.b. (-1)^(-1)=-1≠1.
Dass die Funktion hoch und und runter geht stellt ja kein Problem dar. Dies hat nur zufolge, dass die Funktion nicht stetig ist.
Und ich denke meine Rechnungen sollten richtig sein, mein Taschenrechner sagt mir ebenfalls, dass -1^-1 tatsächlich -1 ergebe.
hier

steht nicht f(-1/3) . Wenn das so wäre ,müsste das Minus auch unter der Wurzel stehen. Da hätte eine Klammer hingehört
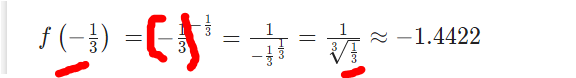
Ja du hast vollkommen recht, allerdings ist das Ergebnis -1.4422 dennoch für f(-1/3) korrekt, da ich im Taschenrechner den richtigen Term mit -1/3 eingegeben habe und beim Rechenweg nur das Minus vergessen hatte.
ich weiß nicht genau , was du meinst
(-1/3)^(-1/3) = ist AUCH ein Ausdruck mit i
siehe hier
principal root und real-valued root werden unterschieden. Den Unterschied kann ich aber nicht erklären
Die Gleichung x=eˡⁿ ˣ gilt nur für x>0. Mit Deiner Argumentation könntest Du genauso zeigen, dass x² nur für x>0 definiert ist.