Hi, ich brauche Hilfe bei einer Mathe Aufgabe?

Die lautet: A = {x€R : E y €R : (x + 2 )^2 + 4 y^2 < 9

Ich soll das sup, min, max und infimum bestimmen und ich habe keine Ahnung, wie ich da anfangen muss.

Answer 1

[LoverOfPi]

Das ist in Worten gefasst die Menge der reellen Zahlen, für die es eine andere reelle Zahl gibt, sodass (x+2)²+4y² < 9.

Offenbar gibt es so eine Zahl gerade dann, wenn (x+2)²<9. Das heißt, genau dann wenn -3 < x+2 < 3.

Ich denke damit kannst du etwas anfangen.

Du kannst das auch geometrisch als (offenen) Ball mit dem Radius 3 um den Punkt (-2/0) interpretieren. Dann solltest du auch darauf kommen.

Woher ich das weiß: Studium / Ausbildung – Ich studiere Mathematik im vierten Semester.

Answer 2

[Clemens1973]

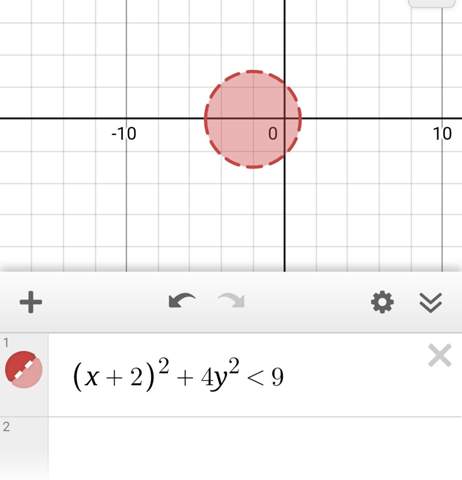
Für die Elemente x aus A muss die Ungleichung gelten

$(x+2)^2<9-4y^2\quad \text{für ein }y\in\mathbb{R}$

Es sollte klar sein, dass das Infinum, Supremum und -falls sie überhaupt exisiteren- Minimum und Maximum erreicht werden für y=0.

Entweder sieht man es gleich, oder sonst noch die Wurzel ziehen und dabei eine Fallunterscheidung machen nach dem Vorzeichen der Klammmer auf der linken Seite.

Comments

[Ghgghhg]

Ich habe für Inf und min -5 und für sup und max 1 rausbekommen. Stimmt das?

[Clemens1973]

@Ghgghhg

Ja, inf A=-5 und sup A=1. Aber bei Maximum und Minimum würde ich nochmals überlegen. LIegen den das Infinum und das Supremum in der Menge A?

Answer 3

[eterneladam]

Überlege dir, um welche geometrische Form es da geht. Lass das in einer App zeichnen oder setze ein paar Werte ein. Dann liegt die Lösung auf der Hand.

Comments

[Ghgghhg]

Ich verstehe nicht, um welche geometrische Form es sich handelt, weil mich das y sehr verwirrt...