Gleichschenkliges Dreieck C?
Kann man bei einem gleichschenkligen Dreieck c ohne die Höhe berechnen?

Also ich habe:
Winkel von A, B, C
Länge von a
ich brauche: c oder h
7 Antworten
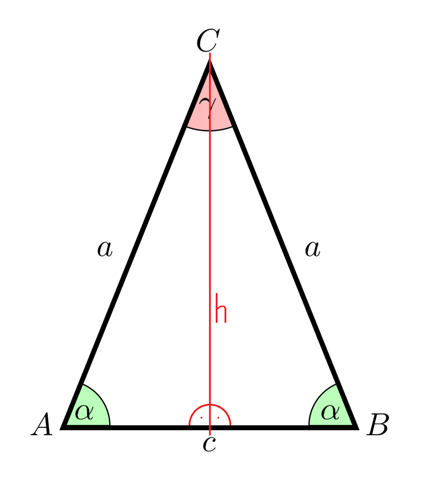
Teile das Dreieck in zwei Hälften mit je einem rechten Winkel:

Wenn Du die Strecke a kennst und den Winkel A (α), so kannst Du über die Winkelfunktionen auch die Höhe h bestimmen.
Vom Winkel A (α) ausgehend wäre a die Hypothenuse (H) und die Höhe h die Gegenkathete (GK), also wird mit dem Sinus gerechnet:
Hast Du die Höhe h, so lässt sich mit dem Satz des Pythagoras die halbe Seite c ermitteln. Für die ganze Seite c gilt dann:
c = 2 · √(a² - h²)
45° sind die beste Voraussetzung, um so eine Aufgabe schnell zu lösen. Denn dann hast Du zwei gleichlange Seiten (h und c/2). Du musst also nur das Hypotenusenquadrat (a²) durch 2 teilen und daraus die Quadratwurzel ziehen. Der Rechenweg hierfür wäre
h = c/2 = √(a² : 2) = √(4,3² : 2) =√(18,49 : 2) = √9,245 = 3,041
Aber auch mit der Formel h = sin α · a sollte das richtige Ergebnis herauskommen:
h = sin α · a = sin 45° · 4,3 = 0,707 · 4,3 = 3,041
Ich vermute mal, dass Dein falsches Ergebnis an einem Bedienungsfehler des Taschenrechners liegt. Nicht jeder Rechner lässt eine Zeichenkette ohne Zwischenergebnis oder Klammern zu.
man kann das mit dem Sinussatz ausrechnen:
a= c * sin(alpha)/sin(gamma)
Hallo,
der Winkel bei C reicht schon.
Nimm einfach den Kosinussatz, der in beliebigen ebenen Dreiecken gilt:
c²=a²+b²-2ab*cos (gamma).
Im Falle a=b:
c²=2a²-2a²*cos (gamma).
Anschließend nicht vergessen, die Wurzel zu ziehen.
Herzliche Grüße,
Willy
Vielen Dank! Aber das kommt bei mir nicht hin...
Z.B ist gamma 120 und a 4.3, dann ist c 2.6?
Kosinussatz: https://de.wikipedia.org/wiki/Kosinussatz#Allgemeine_Formulierung
Im gleichschenkligen Dreieck ist a=b
c² = a² + a² - 2a² • cos(γ) = 2a² • (1 - cos(γ))
c = a • √(2 • (1 - cos(γ)))
Kann man. Zerlege das Dreieck in zwei rechtwinklige Dreiecke. a ist die Hypothenuse, h und 1/2c die Katheten. Die Winkel kennst Du. Die Formeln mit den Winkelfunktionen mußt Du dir dann schon selbst raussuchen, die weiß ich auch nicht auswendig :-)
Nö. Du kennst ja alle Winkel. Und die Formeln
https://de.wikipedia.org/wiki/Trigonometrische_Funktion
kann man umstellen.
Jetzt kommst Du bestimmt von alleine drauf.
Die Winkel- und Längenbeziehungen am rechtwinkligen Dreieck sind wichtiger, als man zunächst glaubt. Da baut vieles in Vermessung, Konstruktion und Bau/Statik auf. Es ist wichtig, dass Du das dann auch verstehst und die Formeln findest und umstellen kannst.
Viel Erfolg ... laß den Kopf rauchen :-)
Das ist die beste Antwort aber irgendwas mache ich falsch...
Wenn ich Alpha = 45° und a (also H) = 4.3 dann bekomme ich als Höhe (GK) 3.65 raus, was nicht sein kann, weil ich das Dreieck gezeichnet habe und gemessen habe (GK bzw Höhe = 2.9)