Extremwertprobleme Rechteck?
Hi,
kann mir vielleicht jemand bei der Aufgabe helfen , ich verstehe die nicht . Wirklich ich habe alles versucht,aber leider komme ich nicht weiter. Auch chatgpt hab ich versucht zu fragen , aber der kann es irgendwie nicht lösen, es wäre sehr sehr nett von euch . Vielleicht auch ein paar sätze zur Erklärung,
danke im voraus 🙏

3 Antworten
Du hast also einen Punkt (x₀|y₀) = (4|2) gegeben und willst ein Rechteck bauen, dessen gegenüberliegender Eckpunkt auf f(x)=1/x liegt. Dieser Eckpunkt hat also dann die Koordinaten (x|¹/ₓ), und die Seitenlängen des Rechtecks sind x₀−x und y₀−¹/ₓ.
Jetzt willst Du entweder Fläche oder Umfang des Rechtecks maximieren. Dabei betrachten wir x (also die x-Koordinate des gewählten Punkts auf der Funktion) als Variable:
- Die Fläche ist Seite×Seite, also A(x)=(x₀−x)⋅(y₀−¹/ₓ) = x₀y₀ − xy₀ − x₀/x + 1. Wenn Du das differenzierst, bekommst Du A’(x)=x₀/x²−y₀. Das kannst Du Null setzen und bekommst den gesuchten Wert für x=√(x₀/y₀)=√2. Der gesuchte Punkt ist also P₁(√2|½√2), und der Flächeninhalt ist A=(x₀−x)⋅(y₀−¹/ₓ)≈3.34
- Der Umfang ist 2⋅(Seite+Seite), also U(x)=2x₀+2y₀−2x−²/ₓ. Wenn Du das ableitest, dann kommt U(x)=²/ₓ−2 heraus, und die gewünschte Nullstelle ist x=1, der Punkt ist also P₂(1|1), und der Umfang beträgt U(x)=2x₀+2y₀−2x−²/ₓ=8
- Den Kokolores mit der zweiten Ableitung kannst Du selber machen.
Die beiden Funktionen für Umfang und Flächeninhalt als Funktion des gewählten x-Wertes kannst Du Dir leicht ansehen. Der gewünschte Umfang bzw. Flächeninhalt entspricht dem Funktionswert am Maximum.

Uns so sehen die beiden maximalen Rechtecke aus:

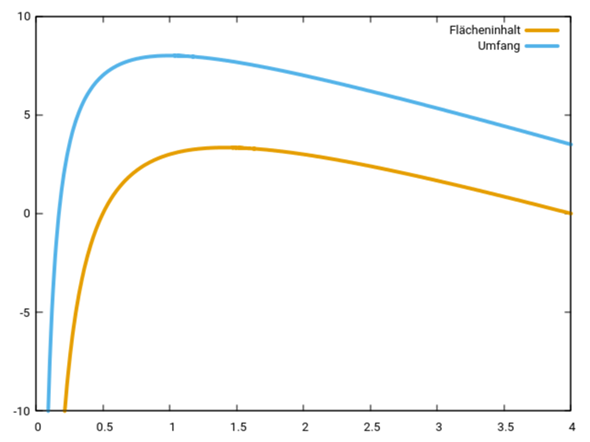
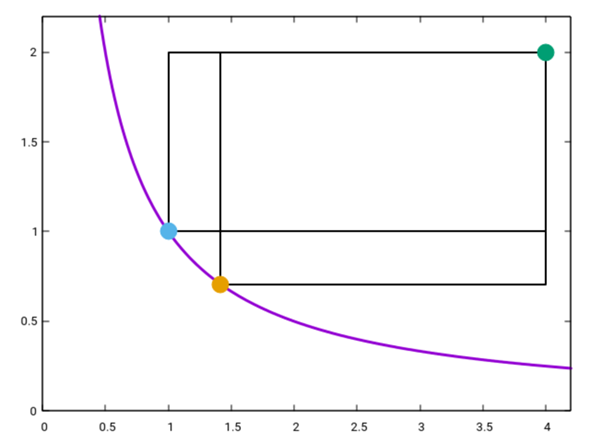
Ich hoffe, daß ich mich beim schnellen Schreiben nicht verrechnet habe. Was hast Du denn wofür heruasbekommen, und wie?
Ich habe noch schnell die Werte für Umfang und Flächeninhalt in die Antwort nachgetragen. Dein Flächeninhalt stimmt.
erpis hat bereits die Funktionen für Fläche und Umfang angegeben
in der Formel muss dann noch f(x) durch 1/x ersetzt werden
hier noch eine Ergänzung:
der eingezeichnete Punkt habe die Koordinaten (x|f(x))
die Breite des roten Rechtecks ist 4-x (also von x bis 4)
die Höhe des roten Rechtecks ist 2-f(x) also von der Höhe des Punktes bis zur waagrechten Linie oben, also senkrecht von f(x) bis 2. Diese Länge ist dann 2-f(x)
bei der Fläche musst du Breite mal Höhe rechnen, beim Umfang 2*Breite+2*Höhe
Welche Maße soll man dann als Lösung angeben ? Hab jetzt den punkt ausgerechnet an dem es maximal ist also (wurzel 2/ 1 :wurzel 2)
der Flächeninhalt ist für x=Wurzel(2) maximal
die Maße des Rechtecks sind dann 2.59 und 1.29 damit wäre der maximale Flächeninhalt 3.35 (deine Lösung ist also richtig)
der Umfang des Rechtecks ist für x=1 maximal
Also ich hab irgendwie als flächeninhalt ca 3,34 cm^2 raus , irgendwie hört sich das falsch an…
Bei a musst du einfach die Funktion
und bei b die Funktion
optimieren und dabei schauen ob das ergebnis im richtigen Intervall liegt.
Vielen dank ich hab aber auch die werte wurzel von 2 und 1/wurzel von 2 als x und y werte aber wenn man die werte einsetzt kommt 3,34 raus…