Wie schreibe ich die Punkt-Neigungs-Form?

Hallo,

in Mathematik haben wir folgende Aufgabe bekommen:

" Schreiben Sie die Punkt-Neigungs-Form (Statt Neigung kann man auch Steigung benennen) der Gleichung der beschriebenen Linie."

Wir haben einen Punkt gegeben, der "durch" geht : P(4,2) und eine Gleichung, die "Parallel" ist : y= (-3/4 x ) - 5

Soll ich nun für Y= 2 einsetzen und für X=4? Oder wie genau soll ich vorgehen? Wenn der Punkt durch "etwas" geht, und die Gleichung "Parallel" ist, dann ist das nicht die Gleichung, die zu dem Punkt passt, oder?

Vielen Dank für eure Hilfe

Answer 1

[Halbrecht]

Wir haben einen Punkt gegeben, der "durch" geht : P(4,2) und eine Gleichung, die "Parallel" ist : y= (-3/4 x ) - 5

die Gerade ist parallel
parallele Geraden haben dieselbe Steigung ( hier -3/4)

Daher kann man schreiben ( erstmal ohne P )
y = -3/4 * x + b

fehlen y , x und b

aber wir haben ja P! mit P(x/y)

4 = -3/4 * 2 + b
4+6/4 = b
16/4 + 6/4 = 22/4 = b

Comments

[Mayuuuuu2001]

Muss es nicht andersrum sein? Denn bei einem Punkt wird erst der X Wert genannt und dann der Y-Wert. X=4 , Y=2

Also...

2= (-3/4) • 4 + b

2= -3 + b | +3

5= b

Also y= (-3/4 x) + 5

[Halbrecht]

@Mayuuuuu2001

Wie wahr , wie wahr : natürlich war ich voll falsch

2 = -3/4 * 4 +b

2 + 12/4 = b

5 = b

sorry

aber du scheinst ja was verstanden zu haben :!!:)

[Mayuuuuu2001]

@Halbrecht

Ist an sich nicht kompliziert, mich hat einfach die Aufgabenstellung übelst irritiert XD. Dankeschön

Answer 2

[verreisterNutzer]

wie genau soll ich vorgehen?

Du musst wissen, dass dass due Steigung Deiner gesuchten Geraden gleich Deiner gegebenen Geraden ist. Daher:

$f\left(x\right)=-\frac{3}{4}x\ +b;\ f\left(4\right)\ =2\ \to b\ =\ 2+3\ =5$

Damit ist berechnest Du die Nullstelle zu:

$-\frac{3}{4}x+5\ =\ 0\ \to x\ =\frac{20}{3}$

Die Punkt-Neigungs-Form ist dann:

$f\left(x\right)\ =-\frac{3}{4}\left(x-\frac{20}{3}\right)+c;\ f\left(4\right)=\ 2\ \to c=0$

Also

$f\left(x\right)=-\frac{3}{4}\left(x-\frac{20}{3}\right)$

Skizze:

Comments

[Mayuuuuu2001]

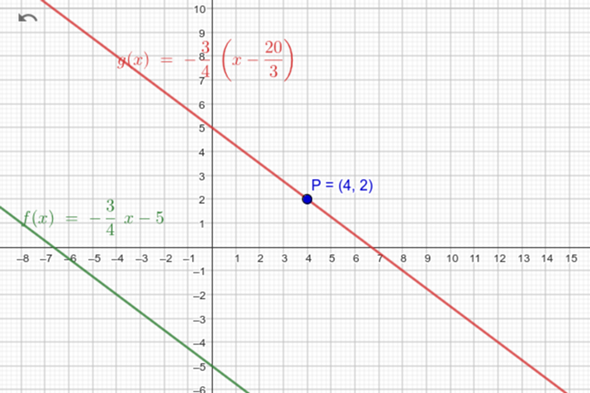
Um ehrlich zu dein verwirrt mich das😅.

Nullstellenberechnung hatten wir z.B. noch gar nicht. Mit f(x) arbeiten wir auch noch nicht, nur y=....

Also, da sie Parallel sind, haben sie die gleiche Steigung. Soweit verstanden.

Das heißt, wir suchen nur noch b, also den Y-Achsenabschnitt.

Kann ich dann nicht, wie in der unteren Antwort, für y=2 und x = 4 einsetzen?

Sodass 2= (-3/4) x 4 + b habe?

Sprich: 2= -3 + b | +3

5= b

Also y= (-3/4 x) + 5