was ist falsch bei der?

Answer 1

[Schachpapa]

Der Ansatz.

Das 6fache von x ist 6x, das Quadrat ist x²

Wenn das 6fache der Zahl um 9 größer sein soll als ihr Quadrat, lautet die Gleichung

6x=x²+9

Answer 2

[verreisterNutzer]

was ist falsch bei der?

Deine Grundgleichung ist falsch:

Eine Zahl: x
Das Sechsfache: 6x
das Quadrat der Zahl: x²

Das Sechsfache ist um 9 größer als x² heißt, dass man zu x² die Zahl 9 addieren muss, um auf 6x zu kommen, also:

$6x=x^2+9$

Hinweis zur Lösung: Es lohnt sich, genau hinzusehen, um beispielsweise die Anwendung der pq-Formel zu vermeiden.

Answer 3

[Leamu186516]

Ich weiß nicht genau, aber kann

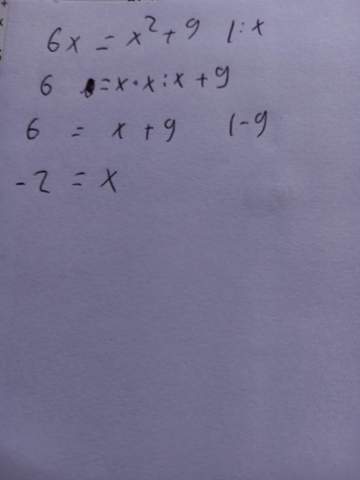
dieses hier stimmen?

LG und noch ein schönes Wochenende

Comments

[LoverOfPi]

Nein, daran ist so ziemlich alles falsch.

[verreisterNutzer]

Ich weiß nicht genau, aber kann ... dieses hier stimmen?

Nein, das kann nicht stimmen (auf beiden Seiten :x hieße "die ganze rechte Seite geteilt durch x und dann hättest Du rechts ein 9/x stehen. Das führt als zu nichts).

[SebRmR]

Noch ein Fehler: 6 - 9 = -3

Und das -2 nicht die Lösung sein kann (-3 auch nicht), kann man prüfen:

6*(-2) = (-2)² + 9

6*(-3) = (-3)² + 9

Wenn die vermeintlichen Lösungen falsch sind, ist oft der Rechenweg fehlerhaft.

Answer 4

[LoverOfPi]

6x=x²+9 ist die Ausgangsgleichung, nicht 6x²=x+9.

Woher ich das weiß: Studium / Ausbildung – Ich studiere Mathematik im vierten Semester.