Surjektiv und nicht injektiv?
Hallo, ich Kämpfe seit ner Ewigkeit mit dieser Aufgabe. Ich habe schon ein Pfeildiagramm gezeichnet um es zu verstehen. Paßt auch aber ich finde keine Funktion f(x) die relativ einfach ist. Da ich sie dann auch beweisen muss das sie subjektiv und nicht Injektiv ist.

Ich danke schonmal für die Hilfe
3 Antworten
Ich würde einfach...
... verwenden.
Wegen f(1) = 1 = f(2) ist die Funktion nicht injektiv.
Da man zu jedem b ∈ ℕ ein a ∈ ℕ mit f(a) = b findet (da man jeweils a = b + 1 wählen kann), ist die Funktion surjektiv.
Anschaulich:

Jede Zahl in der Zielmenge wird getroffen. [Surjektivität]
Es gibt zwei Zahlen (nämlich 1 und 2), die auf die gleiche Zahl in der Zielmenge (nämlich 1) abgebildet werden. [Nicht-Injektivität]
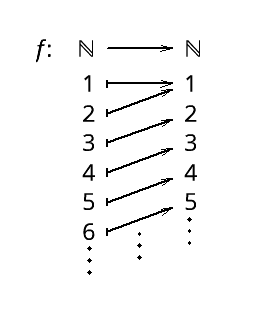
Der Vorschlag von mihisu ist naheliegend und einfach, wenn es etwas komplizierter sein darf,
f(2n-1) = 2n-1,
f(2n) = n,
für n= 1, 2, 3, ....
Ich würde einfach eine Normal Parabel nehmen und diese dann in z.T. in den ersten Quadranten verschieben. Somit wäre eine mögliche Funktion f(x)=(x+1)².
Surjektivität und Nicht-Injektivität kannst du dann mithilfe der Definitionen leicht beweisen bzw. Widerlegen
Sorry, ich meinte (x-1)². Hab mich im Vorzeichen vertan. Aber du hast Recht, sie ist natürlich nicht surjektiv
Hilft nicht. f(1)∉ℕ, und die Bilder von Nicht-Quadraten (2, 3, 5, ...) fehlen immer noch.
f ist auf ℕ injektiv, aber nicht surjektiv: f(ℕ) = {4, 9, 16, 25, ...}