Welche dieser funktionen sind bijektiv, surjektiv oder injektiv?
2 Antworten
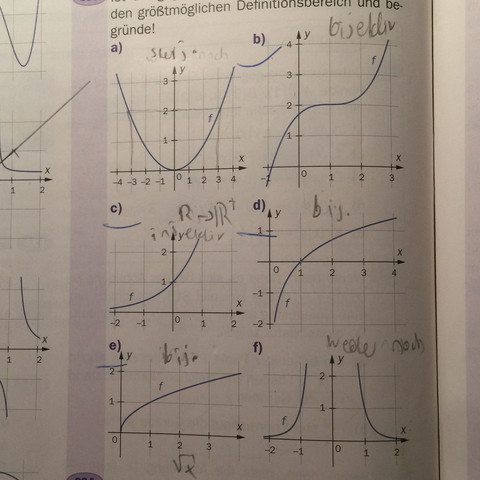
a) ist nichts. Im negativen y-Bereich existieren keine Urbilder, während im positiven für jeden Wert 2 existieren.
b) ist bijektiv. Für jeden y-Wert findet sich genau ein x-Wert.
c) ist injektiv. Im negativen y-Bereich existieren keine Urbilder, im positiven für jeden aber genau eins.
d) ist wieder bijektiv. Wie gesagt. Für jeden y-Wert genau ein x-Wert.
e) ist injektiv. Die Funktion ist im negativen Bereich nicht definiert. Im positiven Bereich hat jedoch jeder y-Wert einen korrespondierenden x-Wert (Anhand der Skizze meine ich es handelt sich um eine Wurzelfunktion)
f) ist wieder nichts. Gleiche Begründung wie bei a)
PS:
Das alles unter der Prämisse, dass "größtmöglicher Definitionbereich" heißt "reelle Zahlen"... eigentlich könnte man das noch erweitern auf den komplexen Zahlenbereich und dann wären die Lösungen anders...
Wenn a eine Funktion von R auf R ist, dann ist sie gar nichts.
Ist a aber eine Funktion von R auf R+, dann ist sie surjektiv. Weil dann jedes Element von R+ MINDESTENS EIN Urbild hat. Das heißt die Surjektivität hängt von der Bildmenge ab.
Leider ist der Aufgabentext nicht vollständig lesbar.