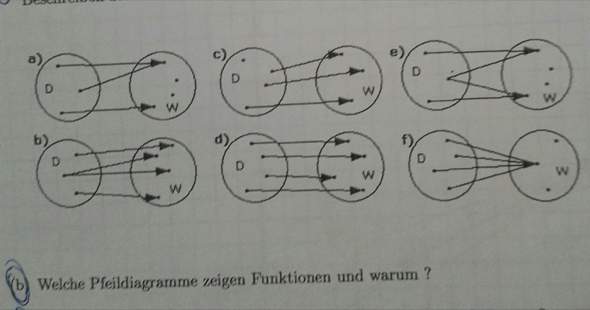
Welche Pfeildiagramme zeigen Funktionen und warum?
Es gibt die surjektive, die injektive und die bijektive Funktion. Soweit ich weiß, stellt d) eine bijektive Funktion dar, die umkehrbar ist. a), b), c), e) und f) sind keine Funktionen. Ist meine Aussage korrekt oder irre ich mich?
2 Antworten
Hallo,
wenn durch Pfeildiagramme Funktionen definiert werden, dann kannst du immer die Diagramme ausschließen, in denen von einem Element zwei Pfeile ausgehen. Solche Diagramme stellen keine Funktion dar.
Stell dir es folgendermaßen vor:
Ich definiere die "Funktion" f : 1 → 2 und 1 → 9, also f(1) = 2 und f(1) = 9.
Das wäre so eine Situation : von der 1 gehen zwei Pfeile weg, einer auf die 2 und ein zweiter auf die 9.
Man fragt sich dann: ja was ist denn f(1) nun, zwei oder neun??
Die Antwort wäre: beides.
Solche Zuordnungen will man für Funktionen nicht haben, weil man sich damit in Widersprüche verstricken würde, wie z.B
f(1) = f(1) (weil 2 = 2), aber auch
f(1) ≠ f(1) (weil 2 ≠ 9).
Also wäre eine Aussage und ihr Gegenteil wahr, für Mathematiker der Horror. ;-)
Gruß
funktionen sind eindeutige zuordnungen.
dh. dass einem element auch nur ein element zugordnet wird.
bei manchen dieser bilder siehst du wie von einem element zwei oder mehr pfeile abgehen also dass einem element zwei oder mehr elemente zugeordnet sind. das sind dann keine funtionen. also b und e
hm.. also welche Pfeildiagramme stellen nun eine Funktion dar?