Summen zusammenfassen (Summenzeichen)?

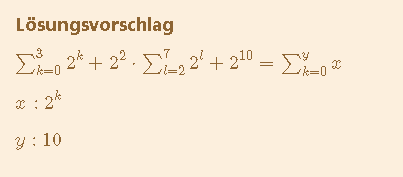
Kann mir jemand erklären wie man auf das Ergebnis kommt?
1 Antwort
Schreibe mal jede Summe einzeln aus, dann wirst du die Intuition dahinter verstehen.
Lösung:


nicht unbedingt ausrechnen aber die summen ausschreiben, so dass sie vollständig dastehen
so wie du potenzen z.b a^3 = a * a * a ausschreiben kannst
Ich komme leider immer noch nicht weiter. Muss man da eine Indexverschiebung machen?
wenn du es korrekt ausschreibst, dann kannst du von dem gesamten wieder die Summe bilden, was der Lösung entspricht. Darauf wollte ich hinaus.
Wie komme ich aber auf den Startwert 0 und Endwert 10 ohne vorher die Lösung zu kennen?
Das sieht man direkt wenn man es ausschreibt, kannst du vllt ein Screenshot von dem machen wie du es ausgeschrieben hast?
ich habe bisher einfach nur 2^10 und 2^2 ausgeschrieben. Ich wusste leider nicht was ich da noch mehr hätte machen sollen :/
Ok, ich meinte damit dass du da jeden einzelnen Term also auch die Summen hinschreibst.
Z.b ist die summe von k = 0 bis k = 3 von 2^k
= 2^0 + 2^1 + 2^2 + 2^3
Ah. Ja das habe ich noch nicht gemacht. ich versuch es mal. Danke für die Hilfe :)
Habe beide Summen ausgeschrieben und habe jetzt halt zwei Terme mit ganz vielen Potenzen mit Basis 2, die mit einander multipliziert werden könnten.
Hab dir die Lösung hingeschrieben. Ging darum dass wenn du 2^2 in die Summe die von 0 bis 7 geht reinmultiplizierst, dann siehst du was passiert weil ja a^2 * a^2 = a^(2+2) = a^4 etc. ist
Danke. Mir ist gerade aufgefallen warum ich es nicht verstanden habe. Ich dachte die 2^2 gehört in den Summanden der ersten Summe
Ja, sorry. Habs jetzt verstanden. Ich dachte bei beiden Summen, dass die Potenzen noch in die Summe gehören. Wäre da aber eine Klammer drum dann würde 2^2 und 2^10 in die Summe reingehören oder?
Übrigens kannst du es auch direkt in die Summe reinmultiplizieren, musst dann nicht den index verschieben sondern da steht dann 2^k+2. Aber dadurch dass man es ausschreibt sieht man besser wieso das ist
Hab das bild geupdated. Die plusse trennen die Terme. Es stimmt aber schon dass es evtl. verwirrend aussieht, aber jetzt sollte es klar sein
Ah, denkst du man sollte die erstmal ausrechnen. Habe die ganze Zeit überlegt wie ich die Terme umformen könnte.