Sinusfunktion mit bestimmten Nullstellen?
Ich möchte eine Sinusfunktion haben, die an bestimmten Stellen ihr Vorzeichen wechselt. Am besten sollte der Abstand von Nullpunkt zum nächsten Nullpunkt immer das 0,6-Fache des Vorherigen Abstandes sein. Eine Sinusfunktion soll es sein, damit ich das ganze danach verschieben kann.
Durch bloßes Ausprobieren bekomme ich es leider nicht hin.
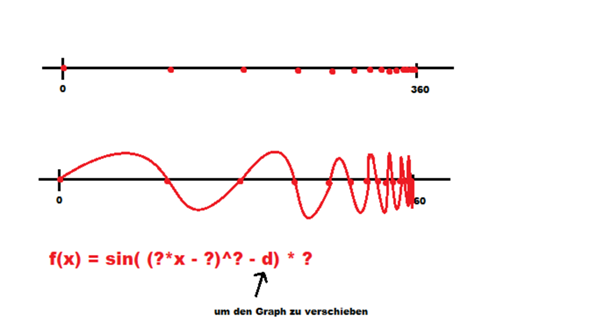
Weiß wer, wie man da auf eine Formel kommt? Dass man das x hoch irgendwas nehmen muss, damit die Abstände immer kleiner werden, hab ich schon gecheckt. Mehr aber auch nicht.
5 Antworten
Schwierig. Das wird nämlich so nicht funktionieren mit einem "Polynomsinus". Wofür brauchst du so eine Funktion denn genau?
Die Frage, die sich dabei stellt, ist wie du dir die Funktion vorstellst. Wenn sich der Abstand zur nächsten Nullstelle immer ver-0,6-facht und wählen wir als Anfangswerte zum Beispiel 0 und 1, werden sich die Nullstellen irgendwann vor 2,5 sammeln, denn die "Nullstellenfolge"
konvergiert dann monoton wachsend gegen 2,5. Auch bei anderen Anfangswerten wird die Folge nicht divergieren, die Nullstellen verteilen sich also nicht auf den gesamten Definitionsbereich. Warum soll denn es ein Sinus sein?
wär gut wenn es bei ~380 divergiert
Verstehe ich nicht.
In der Antwort von mihisu findest du aber eine mögliche Funktion. Ich habe von Spieleentwicklung nicht viel Ahnung, aber was genau willst du mit dem Sinus modellieren? Die Position der Grasstreifen?
Mein Fehler, 360 passt schon.
Die Farbe des Streifens soll sich bei jedem Nullpunkt ändern.
Ich male quasi den Bereich von x=0 bis x=Erste Nullstelle dunkelgrün aus. Dann x=Erste Nullstelle bis x=Zweite Nullstelle Hellgrün, usw.
Wenn man das ganze dann um 90 Grad (CCW) dreht entsteht so ein Bild wie ich es dir geschickt habe. Es erzeugt eine Art 3D-Illusion, da die Streifen kleiner werden, je "weiter sie weg sind" / je höher auf dem Bildschirm sie sind / je höher x ist. Und das coole ist: Da es ein Sinus-Graph ist, den ich ja mit einem + z in der Klammer verschieben kann, kann ich das Gras "auf einen Zulaufen lassen".
Dann reicht dir aber auch einfach die Folge oben. Da brauchst du keinen Sinus für. ;-)
Du suchst vermutlich sowas wie...
Da ist der Abstand von zwei benachbarten Nullstellen immer genau das 0,6-fache des vorigen Nullstellenabstands.
Das kann man beispielsweise so herausfinden...
https://www.dropbox.com/s/lppg2ota908652f/sin06.pdf?dl=0
Da habe ich dir mal aufgeschrieben, wie in etwa meine Vorgehensweise gewesen ist.
Sagen wir, xi wären die Nullstellen.
x0=0
x1=Pi
Der Abstand ist
x1-x0=Pi
Nächste Nullstelle müsste dann so liegen dass
0,6(x1-x0)=x2-x1 ist
also gilt:
x2-x1=0,6x1-0,6x0
oder
x2-1,6x1+0,6x0=0
x2=1,6x1-0,6x0
statt den indizes 0,1,2 kann man genauso gut n, n+1 und n+2 nehmen.
Was ich aber grundsätzlich betrachten würde:
google sagt dass man eine funktion f(x) stauchen kann indem man einen Faktor
a*x stattdessen benutzt:
Hierbei geht es um eine gleich große Stauchung der kompletten Funktion.
Was ich allerdings ausprobieren würde:
ich würde einfahc mal sagen: Sei die Stauchung doch abhängig von x!
also a(x) dort einsetzen.
Und je größer x wird, desto größer sollte auch a sein (denn je größer a, desto größer die Stauchung!)
Daher würde ich doch einfach mal sagen dass wir f(a(x)*x betrachten und versuchen, eine regel für a(x) zu finden.
wir wissen dass gilt:
x0=0
x1=pi
(ab hier wirds interessant)
x2=1,6x1-0,6x0=1,6Pi-0,6*0=1,6*Pi
x3=1,6(1,6Pi)-0,6(Pi) =Pi*(1,6^2-0,6)
x4=1,6*Pi*(1,6^2-0,6)-0,6*1,6*Pi
=Pi*(1,6^3-2*0,6*1,6)
x5=1,6*Pi*(1,6^3-2*0,6*1,6) -0,6*Pi*(1,6^2-0,6)
=Pi*(1,6^4-2*0,6*1,6^2-0,6*1,6^2+0,6^2)
=Pi*(1,6^4-3*0,6*1,6^2+0,6^2)
x6=1,6*Pi*(1,6^4-3*0,6*1,6^2+0,6^2) -0,6*Pi*(1,6^3-2*0,6*1,6)
=Pi*(1,6^5 -3*0,6*1,6^3 +0,6^2*1,6 -0,6*1,6^3+2*0,6^2*1,6 )
=Pi*(1,6^5 -4*0,6*1,6^3 +3*0,6^2*1,6)
es wäre natürlich praktisch wenn wir hueraus eine passende regel finden könnten.
hierzu müssten wir ausgehend von der gleichung
x_n+2=1,6x_n+1-0,6x_n
eine explizite Formel für x_n finden.
ähnelt mir irgendwie den Fibonnaci zahlen, wenn man lange genug dsucht, findet sich da bestimmt auch hierfür eine Lösung.
Auf jeden Fall aber muss gelten dass
f(a(xi)*xi)=0 ist.
da ausser bei x0 überall xi ungleich 0 gilt, so muss demnach bei den Nullstellen a(xi)=0 gelten.
Weiter weiß ich aber auch nicht :-D
Eins von vielen Beispielen solcher Sachen ohne kosntante Periode wäre bspw.
sin(e^x)
hier ist eben sin(a(x)*x) mit
a(x)=e^x/x
Problem ist nur wie du so ein a(x) passend findest damit die Nullstellen der Formel
x_n+2=1,6x_n+1+0,6x_n genügen :-/
Das würde ich in drei Teilschritten lösen.
- Du weisst, dass die Nullstellen des Sinus bei m * pi liegen mit m aus Z.
- Du willst jetzt, dass die Nullstellen woanders liegen. Beschreibe erstmal korrekt, wo die liegen sollen, denn dafür habe ich in deiner Frage noch keine Formel gesehen, nur eine Beschreibung. Sagen wir mal, die n-te Nullstelle sei x_n.
- Dann musst du schauen, dass du eine Funktion findest, mit der du x_n auf n*pi abbilden kannst.
Schau' mal, ob du das hinbekommst.
mit deiner Standardsinusformel kriegt man es nicht hin, weil sie eine konstante Periode hat .
Du möchtest aber eine fkt , bei die Periode nicht eine ganze ist , sondern verkürzt , und dazu wird die Periodenbreite immer geringer.
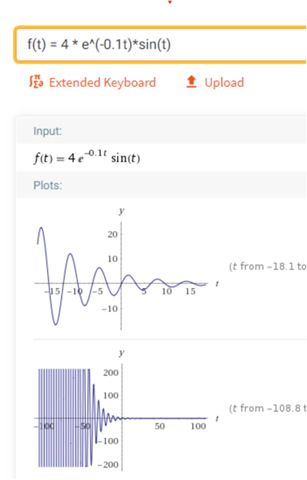
du möchtest etwas ähnliches wie das :
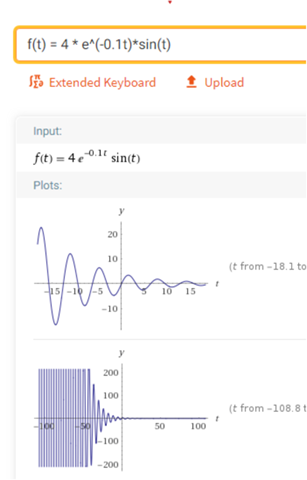
und dazu noch das ganze im + Bereich und mit überall der gleichen Amplitude.
Kann sein , dass man das nur abschnittsweise hinbekommt.
Mal sehen , welcher studierte Mathematiker das Problem lösen kann.
Jo, das passt wenn sie sich sammeln, wär gut wenn es bei ~380 divergiert, da ich nur die Werte im Bereich von x=0 bis x=360 darstelle.
Es soll ein Sinus sein weil ich nicht wüsste wie ich das anders hinbekommen soll, dass ich die Punkte bewegen kann.
Was ich machen will ist ein Pseudo-3D-Rennspiel, bzw. das Gras des Spiels - Welches sich auf einen zubewegen und wegbewegen kann : Siehe Streifen im Gras : https://superdevresources.com/wp-content/uploads/2014/09/javascript-racer.jpg
Eine Sinusfunktion, welche man ja nach links und rechts verschieben kann, bietet sich da an.