Nullstellenbestimmung einer auf der Y-Achse verschobenen Sinusfunktion
Ich komme nicht weiter bei der Frage, wie ich die Nullstellen einer Sinusfunktion bestimme, die auf der Y-Achse verschoben ist, zb. die Funktion: f(x)=sin(x)+0,5 In diesem Falle haben die Nullstellen ja nicht mehr den gleichen Abstand immer, wenn ich nach 0 hin auflöse bekomme ich immer nur eine Nullstelle raus. Im Internet findet man auch nichts.
Anbei noch ein Bild der Funktion zum besseren Verständniss.
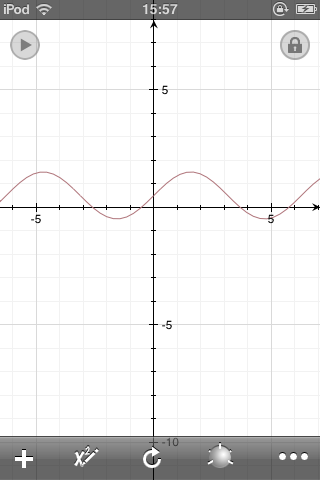
1 Antwort
Naja, erstmal hast du vermutlich den Standard-Ansatz verwendet:
f(x) = 0
=> sin(x) + 0.5 = 0
=> sin(x) = -0.5... Jetzt hast du vermutlich den Arcsin (oder sin^(-1)) benutzt:
x = arcsin (-0.5)
=> x = - Pi / 6.
Nun ist sin(x) + 0.5 noch immer eine 2Pi-Periodische Funktion, d.h. bei
x = -Pi / 6 + 2k * Pi (für eine ganze Zahl k) hat f Nullstellen. Damit hast du schonmal "die Hälfte aller Nullstellen" gefunden.
Nun unterscheidet sich f von der normalen Sinus-Funktion nur um eine Verschiebung nach oben. Dementsprechend liegen die Maxima und Minima der Funktion immer noch bei den selben x-Werten. D.h. bei x = -Pi/2 liegt ein lokales Minimum.
Da die Sinusfunktion achsensymmetrisch ist zu jeder Parallelen der y-Achse, die durch einen Extrempunkt geht, müssen die Nullstellen um -Pi / 2 symmetrisch verteilt sein.
D.h. ich spiegel einfach die Nullstelle bei -Pi/6 an der Geraden x = -Pi / 2 und erhalte eine weitere Nullstelle. Der Abstand von -Pi / 2 und -Pi / 6 ist gerade
-Pi / 6 + Pi / 2 = Pi / 3.
Also muss noch eine Nullstelle bei - Pi / 2 - Pi / 3 = - 5 / 6 * Pi liegen. Auch hier nutzt man wieder das Argument, dass f eine 2Pi-periodische Funktion ist und nun hat man alle Nullstellen gefunden.