Einfache Formel zur Bestimmung aller Nullstellen einer verschobenen Sinus-Funktion?

Moin Leute, folgendes Problem:

Die "normale" Sinus-Funktion sin(x) hat ihre Nullstellen bei:

$\left\{k\pi,\ k\in Z\right\}$ Das lässt sich daraus folgern, dass die Sinusfunktion 2Pi periodisch ist und es genau in der Mitte von 0 und 2kPi auch immer eine Nullstelle gibt. Soweit so gut. Nun möchte ich aber die Nullstellen für eine verschobene Sinus-Funktion der Form sin(x)+a erhalten. Wenn man das einfach gleich 0 setzt, also folgendermaßen:

$\sin\left(x\right)+a=0$ $x=\arcsin\left(-a\right)$ Damit erhält man schonmal eine Nullstelle, da die Funktion wieder 2Pi periodisch ist kann man weitere Nullstellen einfach durch dranhängen von 2kPi bekommen, man hat also Nullstellen bei:

$\left\{\arcsin\left(-a\right)+2k\pi,\ k\in Z\right\}$ Das Problem ist, das sind nicht alle Nullstellen, denn zwischen k=0 und k=1 gibt es eine weitere Nullstelle, nur liegt die in diesem Fall nicht genau zwischen diesen beiden Stellen (außer a ist gleich 0). Ich hab hier mal als Beispiel die Funktion sin(x)+0.5 zeichnen lassen:

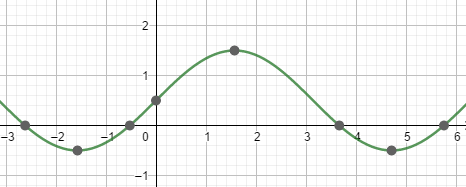
Wenn wir jetzt mal k=0 und k=1 einsetzen erhalten wir als Nullstellen:

x = -1/6pi ≈ -0.5235 und x = 11/6pi ≈ 5.7596

Wenn man den Graph betrachtet sieht man aber, das es eine weitere Nullstelle bei ca. 3.6 gibt, also zwischen diesen beiden Werten. Das Problem ist aber nur, dass anders als bei der normalen sin(x) in diesem Fall die Nullstelle nicht exakt in der Mitte der beiden anderen Nullstellen sitzt. Jetzt ist aber die Frage, wie errechne ich diesen Wert? Es gibt einige "unschöne" Wege wie man das berechnen kann, in dem man zum Beispiel einfach bekannte Nullstellen an einem Tiefpunkt spiegelt, aber meine Frage wäre, ob es eine elegante Formel gibt diese Nullstellen zu bestimmen, was für jedes a funktionieren würde. Gibt es sowas vielleicht? Es geht mir hierbei nicht um ein bestimmtes a, sondern allgemein für alle Werte für a.

Answer 1

[Willibergi]

Schöne Frage!

Wir sind uns sicher schon mal einig, dass die allgemeine Sinusfunktion

$f\left(x\right)=a\cdot\sin\left(b\left(x+c\right)\right)+d$

überhaupt nur Nullstellen hat, wenn gilt:

$\left|d\right|\le\left|a\right|$

(Sonst würde der Graph komplett über oder komplett unter der x-Achse liegen und sie damit nicht schneiden.)

Schauen wir uns erstmal dein konkretes Beispiel an. Ich schreibe dann immer noch die allgemeine Umformung dazu, die kannst du dir ja dann selbst klar machen.

$0=\sin\left(x\right)+0.5\ \Leftrightarrow\ \sin\left(x\right)=-0.5$ $0=a\cdot\sin\left(b\left(x+c\right)\right)+d\ \Leftrightarrow\ \sin\left(b\left(x+c\right)\right)=-\frac{d}{a}$

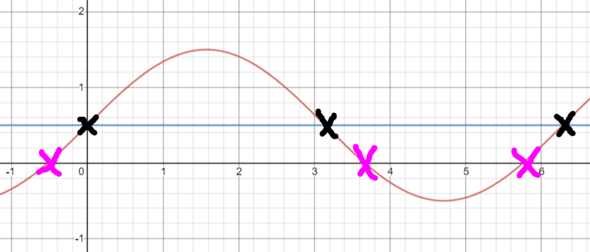
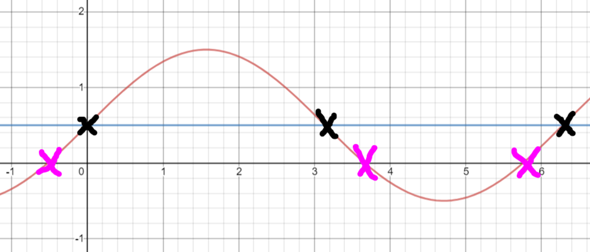
Die Nullstelle, die berechnet werden kann, ist:

$\arcsin\left(-0.5\right)=-\frac{\pi}{6}\approx-0.52$

$x_0=\frac{\arcsin\left(-\frac{d}{a}\right)}{b}-c$

Das ist das linke, pinke Kreuz in der Zeichnung. Der Knackpunkt: Um auf die tatsächliche Nullstelle zu kommen, müssen wir vom linken schwarzen Kreuz (also der eigentlichen Nullstelle, wenn der Graph nicht verschoben worden wäre) um genau arcsin(-0,5) nach links gehen. Vom schwarzen Kreuz in der Mitte hingegen müssen wir um genau arcsin(-0,5) nach rechts gehen, um zur tatsächlichen Nullstelle zu kommen (das pinke Kreuz in der Mitte).

Es gilt also:

$x=0+\arcsin\left(-0.5\right)+2\pi n,\ n\in\mathbb{Z}$ $x_n=0+x_0+\frac{2\pi}{b}\cdot n,\ n\in\mathbb{Z}$

(Das sind die Nullstellen, die hier links von den eigentlichen Nullstellen liegen).

$x=\pi-\arcsin\left(-0.5\right)+2\pi m,\ m\in\mathbb{Z}$ $x_m=\pi-x_0+\frac{2\pi}{b}\cdot m,\ m\in\mathbb{Z}$

(Das sind im Gegenzug die Nullstellen, die hier rechts von den eigentlichen Nullstellen liegen).

Da wir uns in einer Gleichung immer nur auf jede zweite Nullstelle beziehen, multiplizieren wir das n bzw. m mit 2π und nicht mit π.

Generell gilt also:

$0=a\cdot\sin\left(b\left(x+c\right)\right)+d$

hat die Lösungsmenge

$L=\left\{x\in\mathbb{R},\ m,n\ \in\mathbb{Z}\ \ x=x_0+\frac{2\pi}{b}\cdot n\ \vee\ x=\pi-x_0+\frac{2\pi}{b}\cdot m\right\}$

mit

$x_0=\frac{\arcsin\left(-\frac{d}{a}\right)}{b}-c$

Ob das jetzt eine einfache Formel ist, sei mal dahingestellt. Grundsätzlich ist es aber ohnehin in der Regel sinnfrei, Formeln auswendig zu lernen, wenn man das Konzept dahinter nicht anwenden kann (wenn doch, sollte man das bei der konkreten Aufgabe auch tun, wenn sie nicht nur für den Eigenzweck ist).

LG

Comments

[MaxChemieNoob]

Danke vielmals erstmal, aber leider ist das auch nicht ganz das wonach ich suche :(. Mich stört bei der Lösungsmenge das "oder", ich suche nach einer Formel, in der man immer k = 0,1,2,3... etc. einsetzen kann und dann auch die 1. 2. 3. etc. Nullstelle rausfinden kann. Deine Lösungsmenge ist quasi die Verknüpfung zwei einzelner Funktionen, einmal eine Funktion welche die Punkte links von den eigentlichen Nullstellen hergibt und eine die dasselbe für die rechten Punkte macht. Ich möchte aber eine Gleichung, welche quasi beides in sich enthält, versteht du was ich meine? Klar, deine Lösung funktioniert einwandfrei und ist einfach anzuwenden, aber ich möchte es noch simpler und noch eleganter :D

[Willibergi]

@MaxChemieNoob

Puh, da muss ich nochmal überlegen, wie man das arrangieren könnte. Etwas wie hier http://mathb.in/36413 wird dir wohl nicht reichen, oder? Wofür brauchst du die Formel denn?

[MaxChemieNoob]

@Willibergi

Einfach aus Interesse

[Willibergi]

@MaxChemieNoob

Dann wird ja wohl auch die verlinkte Formel reichen ;-)

[MaxChemieNoob]

@Willibergi

Ja, eigentlich reicht es schon ^^

Answer 2

[Tannibi]

Irgendwas verwechselst du. Du meinst nicht

sin (x) + a

sondern

sin (x+a)

Comments

[MaxChemieNoob]

Nee, bei sin(x+a) kann man alle Nullstellen genauso wie bei sin(x) bestimmen, also {kpi - a} würden alle Nullstellen geben, der Abstand benachbarter der Nullstellen ist bei sin(x+a) immer gleich groß, bei sin(x)+a ist das aber nicht der Fall, deswegen muss man da irgendwie anders rangehen wenn man das berechnen will