Kennst du Vomex? Das ist derselbe Wirkstoff, hier eben nur von einer anderen Marke (ratiopharm).
Bei Elvanse (Lisdexamfetamin) ist das kein Problem. Wichtig ist nur, dass der die Kapsel (oder eben deren Inhalt) oral eingenommen, also geschluckt wird, ansonsten wirkt es nicht.
Lisdexamfetamin ist ein Prodrug und per se erstmal wirkungslos. Der aktive Wirkstoff ist das Dexamfetamin, in das Lisdexamfetamin durch hepatische Metabolisierung umgewandelt wird.
Der springende Punkt ist also: Das Lisdexamfetamin muss durch die Leber. Denn nur die Leber kann daraus den aktiven Wirkstoff Dexamfetamin extrahieren, sodass dieser dann ins Blut aufgenommen wird. Soll heißen: Dexamfetamin im Blut wirkt. Lisdexamfetamin im Blut tut nichts.
Bei oraler Einnahme (Schlucken) passiert das Lisdexamfetamin erst den Magen, dann den Darm und durchquert anschließend die erste Leberpassage, wo obige Aktivierung geschieht. Das Endprodukt wird dann erst in den Blutkreislauf aufgenommen (nämlich Dexamfetamin wie gewünscht anstatt Lisdexamfetamin selbst).
Umgehen kann man die Leberpassage z.B. durch nasale ("Ziehen") oder rektale Einnahme. Dadurch kommt allerdings auch keine Wirkung zustande.
Lange Rede, kurzer Sinn: Ob Elvanse-Kapsel oder Elvanse-Pulver ist egal, Hauptsache du schluckst es ganz normal. Alle anderen Experimente (Ziehen, Spritzen, etc.) führen zu Wirkungslosigkeit.
Ich wünsche dir alles Gute.
Das ist völlig richtig. Schmerztabletten unterdrücken den Schmerzreiz, bekämpfen aber die Ursache nicht.
Dafür sind sie aber auch nicht gedacht. Die klassischen "Haushalts-Schmerzmittel" wie Ibuprofen, Paracetamol, etc. sind zu einem großen Teil für temporäre Schmerzen gedacht, verursacht durch Verletzungen, die der Körper z.B. mit der Zeit selbst heilen wird – etwa eine schmerzende Wunde oder ein Knochenbruch. Hier bekämpft der Körper die Ursache selbst, aber das braucht natürlich Zeit. Und um während des körpereigenen Heilungsprozesses nicht täglich die Schmerzen der "Restverletzung" durchleiden zu müssen, könnte man zu Schmerzmitteln greifen.
Gleichermaßen kann die Notwendigkeit auch bei Verletzungen bestehen, die der Körper nicht selbst heilen kann – in diesem Fall sind Schmerzmittel ein Begleitmedikament. Bei einer Krebserkrankung hilft es natürlich nichts, die Tumorschmerzen lediglich durch Schmerzmittel zu unterdrücken. Aber begleitend zu einer "ursächlichen" Chemotherapie sind Schmerzmittel vorübergehend durchaus indiziert.
Lange Rede, kurzer Sinn: Schmerztabletten haben den Sinn, nebenbei zu helfen und einen separat ablaufenden Heilungsprozess weniger unangenehm zu gestalten. In dem Sinne heißt es eher "wenn man die Tabletten nicht mehr einnimmt, hat sich der Schmerz bereits aufgelöst" – idealerweise.
Ich wünsche dir alles Gute.
Oh ja und das ist auch gut so.
Flunitrazepam/Rohypnol ist absolut kein Spielzeug. In die falschen Hände geraten sollte es auf keinen Fall.
Das mag zwar auf den ersten Blick naheliegen, stimmt aber nicht zwangsläufig.
Cmax ist der Spitzenspiegel des Wirkstoffs im Blutplasma. Dieser korreliert zwar in der Regel mit der Wirkstärke, aber nicht immer direkt proportional.
Zunächst sprechen wir bei Cmax über den Spiegel im Blut. Das Blut ist aber oft gar nicht der Wirkort, sondern nur ein Transfermedium. Von der Resorption im Dünndarm bis hin zur endgültigen Entfaltung der Wirkung am Wirkort ist es oft noch ein weiter Weg – bis etwa ein Neuroleptikum das zentrale Nervensystem durchquert, an den postsynaptischen Dopamin D2-Rezeptoren angekommen und angedockt und dann seine antagonistische Wirkung entfaltet hat, kann der Blutspiegel schon längst wieder unter Cmax gefallen sein.
Andere Medikamente (konkret Prodrugs) sind a priori wirkungslos und werden erst durch Metabolisierung (Abbau) in der Leber in einen aktiven Wirkstoff umgewandelt. Das klassische Beispiel ist das ADHS-Medikament Lisdexamfetamin (Elvanse) – würde man das intravenös geben, wäre Cmax direkt erreicht, aber völlig wirkungslos. Die Wirkung entsteht erst durch hepatische Umwandlung zu Dexamfetamin, dem aktiven Wirkstoff.
Eine zeitliche Verschiebung ist aber nicht die einzige Möglichkeit, auch antiproportionale Zusammenhänge existieren ("mehr hilft weniger"), etwa beim Antidepressivum/Schlafmittel Mirtazapin. Hier kann man oft beobachten, dass Dosen zwischen 7,5-15 mg einen deutlich stärkeren sedierenden ("müde machenden") Effekt haben als die höheren Dosen bis hin zu 45 mg. Vermutlich ist das bedingt durch gegenseitige Beeinflussung verschiedener Wirkmechanismen. Der für die Sedierung verantwortliche antihistaminerge Effekt tritt bereits im Niedrigdosisbereich ein, während der noradrenerge (aktivierende, antriebssteigernde) Effekt erst in höheren Dosis zum Tragen kommt und der Sedierung dann entgegenwirkt. Salopp: Niedrige Dosis heißt für die Sedierung freie Fahrt, in hohen Dosen wirkt dieser aber die aktivierende noradrenerge Wirkung entgegen.
Man könnte diese Liste ewig fortführen, Pharmakokinetik ist komplex. Aber eine grundsätzliche Idee, warum das Motto "mehr hilft mehr" in der Pharmakologie oft schiefgeht, ist vielleicht entstanden.
Ich wünsche dir alles Gute.
Wirkstoff, Dosis und Darreichungsform sind entscheidend, der Rest ist nur "Verpackung". Und das stimmt bei beiden Präparaten überein: Quetiapin, 25 mg, Filmtabletten.
Krankenkassen schließen mit Pharmaherstellern Verträge - vereinfacht gesagt läuft das z.B. zwischen der AOK und ratiopharm wie folgt ab: Die AOK versichert "wann immer möglich, bekommen AOK-Versicherte bei Vorlage eines Quetiapin-Rezeptes das Präparat von ratiopharm ("Quetiapin-ratiopharm"), und im Gegenzug gewährt ratiopharm der AOK für Quetiapin-ratiopharm einen Rabatt von 30% (frei erfundenes Beispiel).
Nun sind diese Verträge aber in der Regel auf eine bestimmte Zeit befristet, z.B. auf vier Jahre. Nach diesen vier Jahren schließt die AOK dann neue Verträge, vielleicht mit einem anderen Hersteller als ratiopharm, wenn dieser ihnen ein besseres Angebot macht. Heißt für die AOK-Versicherten: Sie bekommen ab diesem Zeitpunkt nicht mehr Quetiapin-ratiopharm, sondern z.B. Quetialan.
Dem Körper ist das egal - Quetiapin ist Quetiapin. Die ganze Rabattvertrags-Geschichte hat nur einen wirtschaftlichen Zweck.
In deinem Fall hat deine Krankenkasse für den Wirkstoff Quetiapin nun wohl einen Rabattvertrag mit dem Pharmahersteller Gerot-Lannach geschlossen - sodass du Quetiapin in Form des Präparates Quetialan bekommst.
Es ändert sich aber nichts, außer vielleicht Form, Farbe oder Füllstoffe. Die Tabletten enthalten immer noch 25 mg Quetiapin, nur die Marke auf der Verpackung ist eine andere.
Einzig bei Allergikern (z.B. Laktoseintoleranz) spielt der Hersteller manchmal eine Rolle, etwa wenn die eine Marke Laktose als Füllstoff verwendet und die andere nicht. Fällst du darunter nicht, kannst du die Marke aber immer getrost ignorieren.
Ich wünsche dir alles Gute.
Wenn Melatonin alleine nicht reicht und Quetiapin alleine nicht reicht, aber Quetiapin+Melatoni schon, dann bleib doch bei dieser Kombination und alles ist gut oder wo siehst du ein Problem? In diesem Fall ist Quetiapin+Melatonin eben die passende Schlafmedikation für dich und nicht Melatonin bzw. Quetiapin in Monotherapie.
Naloxon kommt bei regulärer Einnahme ohnehin nicht zur Wirkung. Es wird bei oraler Einnahme nach Durchqueren des Gastrointestinaltrakts in der ersten Leberpassage praktisch vollständig eliminiert und wird daher (im Gegensatz zum Tilidin) nicht ins Blut aufgenommen.
Der Grund für die Beisetzung von Naloxon ist die Verhinderung des Missbrauchspotenzials. Opioide werden im Rahmen de Medikamentenmissbrauchs häufig nasal eingenommen oder rektal eingeführt. Dieser Weg befördert den Wirkstoff ohne Leberpassage direkt ins Blut.
Genau diese Einnahmeform wird durch Naloxon allerdings unbrauchbar gemacht: Naloxon ist vereinfacht gesagt schlicht das Gegenmittel zu Opioiden. Soll heißen: Naloxon plus Opioid = Null.
Hier kommt aber der Knackpunkt: Das passiert nur, wenn das Naloxon auch tatsächlich ins Blut aufgenommen wird und zur Wirkung kommt. Bei oraler Einnahme passiert das (durch die Leberpassage wie oben erwähnt) gar nicht erst. Damit wirkt nur das Tilidin wie gewünscht. Bei nasaler oder rektaler Einnahme wird die Leber aber gar nicht erst passiert und der "Spielverderber" Naloxon wird nicht ausgeschaltet. Die Folge: Die volle Dosis Naloxon landet mit dem Tilidin im Blut und hebt die Wirkung von Letzterem auf.
Was passiert nun beim Zerkauen?Das kommt auf die genaue Zusammensetzung der Tablette (insbesondere die genaue Darreichungsform und die genauen Hilfs- und Füllstoffe) an. Schließlich ist eine Tablette zum Schlucken konstruiert (und da wirkt sie auch so wie sie soll) und wenn man sie im Rahmen einer anderen Applikationsform zweckentfremdet, können verschiedene Tabletten verschiedene Wirkungen (oder eben auch nicht) zeigen, auch wenn sie bei oraler Einnahme äquivalent wirken.
Bei einer Retardtablette zerstörst du durch das Kauen natürlich die Retardierung. Das hat zur Folge, dass sich der Wirkstoff schneller freisetzt als er soll und kann zu einem plötzlich zu hohen Blutspiegel und damit zu einer Überdosis führen.
Es kann auch sein, dass die Tablette dann bereits von der Magensäure zersetzt wird und damit gar nicht erst wirken kann. Oder es entsteht Brechreiz durch den Kontakt bestimmter Füllstoffe mit den Geschmacksnerven. Oder unerwartete Nebenwirkungen aller Art treten auf.
Die Rolle des Naloxons bleibt beim Zerkauen (da es sich ja trotzdem um eine orale Einnahme handelt) allerdings gleich und sofern das Tilidin im Blut ankommt, wirkt es auch (wie auch immer).
Lange Rede, kurzer Sinn: Das ist nicht zu empfehlen. Man hat das gar nicht so auf dem Schirm, aber Medikamente sind eine durchdachte technische Konstruktion. Man würde ja auch nicht einfach an einem Flugzeug ein Kabel knipsen, wenn man sich nicht damit auskennt.
Ich wünsche dir alles Gute.
Nach deiner Beschreibung gehe ich davon aus, dass es um eine Depressionsbehandlung geht.
In diesem Fall hilft Aripiprazol nur in Kombination mit einem Antidepressivum. Alleine wirkt Aripiprazol nicht antidepressiv, aber es kann die Wirkung eines gleichzeitig gegebenen Antidepressivums verstärken (wie gesagt: ohne dass es alleine antidepressiv wirkt!).
Wenn selbst ein Antidepressivum plus Aripiprazol nicht ausreichend wirkt, kann man über eine Dosiserhöhung entweder des Antidepressivums oder von Aripiprazol nachdenken.
Theoretisch ist Aripiprazol in einer Dosis von bis zu 30 mg/d zugelassen, allerdings geht man davon aus, dass in der Regel ab 10-15 mg/d bereits alle verfügbaren Rezeptoren besetzt sind und keine Wirkungsverbesserungen mehr eintreten, was auch Studien im System (d.h. Einzelfälle gibt es, die von einer höheren Dosis als 15 mg/d profitieren) belegen.
Soll heißen:
- Falls du bereits ein reguläres Antidepressivum als Basismedikation einnimmst, könnte vielleicht noch eine Dosiserhöhung auf 15 mg/d einen verstärkten Effekt bringen, darüber aber eher nicht mehr. Sprich dazu mit deinem Arzt oder deiner Ärztin über eine Dosiserhöhung.
- Falls du noch kein reguläres Antidepressivum einnimmst, ist die Antwort einfach: Aripiprazol wirkt schlicht nicht antidepressiv. Die antidepressive Wirkung muss bestehen, erst dann kann Aripiprazol sie verstärken. In diesem Fall sprich mit deinem Arzt über die Einstellung auf ein Antidepressivum.
Ich wünsche dir alles Gute.
PS: Eine einfache Metapher: Glutnest + Pusten = stärkere Glut. Pusten ohne Glutnest ist aber völlig wirkungslos. Hierbei steht das Glutnest für das Antidepressivum und das Pusten (= die Sauerstoffzufuhr) für Aripiprazol.
Sowohl Aripiprazol, als auch Olanzapin sind im Kontext der Depressionsbehandlung klassische Wirkstoffe zur Augmentation. Das bedeutet vereinfacht gesagt, dass sie nicht selten zur Wirkverstärkung eines Antidepressivums eingesetzt werden, wenn dieses alleine nur unzureichend wirkt.
Helfen Aripiprazol und Olanzapin also auch alleine gegen depressive Erkrankungen?Nein. Augmentation darf man nicht mit Kombination verwechseln. Bei einer Kombination werden zwei Wirkstoffe mit ähnlicher Wirkung zusammen gegeben, um eine stärkere Wirkung zu erzielen, z.B. zwei Antidepressiva. Bei einer Augmentation hingegen wird zu einem primär wirksamen Wirkstoff (z.B. einem Antidepressivum bei der Depressionsbehandlung) oft ein "fachfremder" Wirkstoff hinzugegeben (z.B. ein Neuroleptikum), der alleine gar nicht die gewünschte (hier: eine antidepressive) Wirkung zeigen würde. Zusammen mit dem primär wirksamen Wirkstoff gegeben, verstärkt der augmentierte Wirkstoff allerdings die primäre Wirkung des primär wirksamen Wirkstoffs.
Im Klartext: Neuroleptika wie Aripiprazol und Olanzapin wirken nicht antidepressiv. Sie können allerdings bei gleichzeitiger Gabe die antidepressive Wirkung eines Antidepressivums verstärken. Dafür braucht es aber ein Antidepressivum.
Um es noch verständlicher zu machen, kann man sich die Augmentation wie die Hinzugabe von Sauerstoff zu einem Glutnest vorstellen. Das verstärkt die "Wirkung" des Glutnests. Ist aber gar kein Glutnest vorhanden, kann man noch so viel pusten wie man will – es wird nicht warm.
Lange Rede, kurzer Sinn: Gegen eine klinische Depression helfen von psychopharmakologischer Seite primär nur Antidepressiva, sie sind die Basis der Behandlung. Ohne Antidepressiva keine (medikamentöse) antidepressive Wirkung. Aufbauend kann man mit Neuroleptika wie Aripiprazol oder Olanzapin augmentieren, aber eben nur, wenn eine Basis besteht.
Ich wünsche dir alles Gute.
Sei
eine Transposition. Das Signum ist definiert als
wobei inv(τ) die Menge der Fehlstände ist. Jedes Paar zweier Zahlen, das nach der Permutation "falsch" herum steht, ist dabei ein Fehlstand. Steht z.B. die 5 nach der Permutation links von der 2, ist (2, 5) ein Fehlstand.
Bei einer Transposition haben wir genau einen offensichtlichen Fehlstand, nämlich (i, j). In der natürlichen Ordnung stand i vor j, die Transposition hat i und j aber getauscht. Ist die Transposition zum Beispiel (25), ist nun 5 das zweite Element und 2 das fünfte. Es ist aber 2 < 5, d.h. 2 müsste links von der 5 stehen - das ist der Fehlstand. Damit enthält inv(τ) genau ein Element, also:
Grundsätzlich musst du bei der händischen Berechnung des Signums tatsächlich alle (geordneten) Zahlenpaare durchgehen - alle. In der symmetrischen Gruppe der Ordnung 5 wären das diese:
Dann überprüfst du für jedes Zahlenpaar, ob es nach der Permutation immer noch in dieser Reihenfolge vorliegt oder es gespiegelt wurde. Wurde es gespiegelt, ist es ein Fehlstand. Am Ende zählst du alle Fehlstände zusammen - sind es gerade viele, ist das Signum 1, sind es ungerade viele, ist das Signum -1.
Eine Alternative ist die Produktformel für das Signum, diese reduziert den händischen Aufwand, ist aber meist mit deutlich mehr Rechenaufwand verbunden.
Tatsächlich ist Tavor Expidet das einzige Lorazepam-Präparat, das in Schmelztabletten vorliegt. Alle anderen Generika gibt es nur in Tablettenform.
Eine Möglichkeit wäre, auf Lorazepam-Tabletten (z.B. Lorazepam-neuraxpharm oder Lorazepam-ratiopharm) auszuweichen und diese zu mörsern. Das ist bei den meisten Lorazepam-Tabletten möglich (Packungsbeilage beachten) und die typische Alternative bei Betroffenen mit Schluckproblemen bei den immer wieder vorkommenden Lieferschwierigkeiten von Tavor Expidet.
Ansonsten bliebe nur eine Umstellung auf einen anderen vergleichbaren Wirkstoff, der in Form von Schmelztabletten lieferbar ist. Das müsstest du mit deinem Arzt besprechen.
Ich wünsche dir alles Gute.
Das stimmt so nicht. Weder zeigen depressive Personen einen Dopamin-, noch einen Serotonin- oder Noradrenalin-Mangel. Diese Hypothesen stammen von vor vielen Jahrzehnten und sind widerlegt.
Näheres dazu hier: Warum wird die These vom chemischen Ungleichgewicht im Gehirn noch regelmäßig bemüht, obwohl sie längt widerlegt ist?
Kurz gesagt: Zwar liegt kein Mangel vor, allerdings helfen Wirkstoffe, die die Konzentration von Serotonin und/oder Noradrenalin und/oder Dopamin erhöhen, nachweislich gegen depressive Erkrankungen. Wie genau, wissen wir bis heute nicht. Man muss aber im Hinterkopf behalten, dass Antidepressiva den Serotonin- bzw. Noradrenalin- bzw. Dopamin-Spiegel über das Normalniveau hinaus heben, d.h. sie bewirken sozusagen eine "Neurotransmitter-Überdosis". Das scheint andere (noch unbekannte) Prozesse anzustoßen, die für eine Linderung der depressiven Symptome sorgen.
Es gibt aber Dopamin-Wiederaufnahmehemmer, zum Beispiel das NDRI Bupropion. Es zieht hinsichtlich der Wirksamkeit aber mit SSRI und SNRI gleich, sodass die zusätzliche Dopamin-Wiederaufnahmehemmung nicht der zentrale Hebel zu sein scheint, der für eine antidepressive Wirkung sorgt.
Mehr zur pharmakologischen Wirkung von Antidepressiva hier: Wie wirken Antidepressiva im Gehirn? Ein neurobiologischer Abriss am Beispiel Mirtazapin
In der Fußnote dieser Antwort findest du nochmal eine ausführliche Darstellung zur These des Neurotransmitter-Mangels.
Ich wünsche dir alles Gute.
Man kann es schon logisch lösen, an eine ernst gemeinte Drittklassaufgabe glaube ich aber nicht.
Wir fangen bei der Blase ganz links an und arbeiten uns im Zickzackmuster durch.
Sei x der Wert der Blase ganz links. Dann hat die Blase darunter den Wert x - 90 und die Blase daneben (in der Mitte) den Wert 260 - x. Bringt uns hier hin:
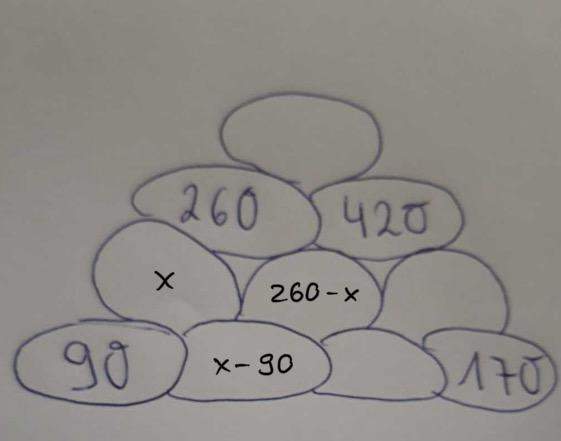
Weiter im Text: Dann hat die Blase rechts unten den Wert
und addieren wir 170 drauf, kommen wir auf den Wert 520 - 2x für die Blase rechts oben. Bringt uns hier hin:
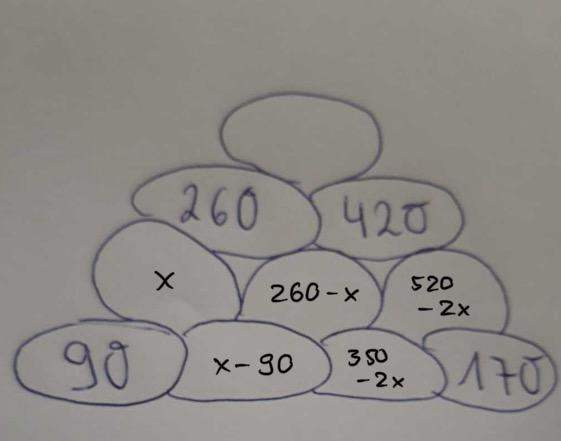
Damit können wir jetzt eine nicht-triviale Gleichung aufstellen, die zum Ziel führt:
Nach x aufgelöst: x = 120
Ab hier lassen sich dann in wirklicher Drittklassmanier die fehlenden Zahlen bestimmen:
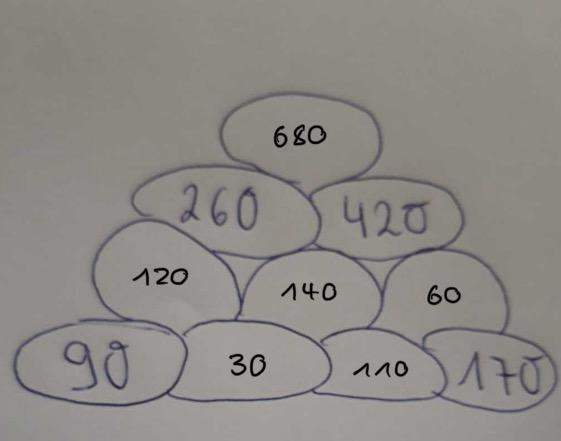
Die kurze Antwort: Bei Sublingualtabletten ja, beim Rest nein.
Gemeint sind hier sog. Sublingualtabletten. Das sind speziell hergestellte, "weiche" Tabletten, die sich im Speichel sofort auflösen und dann über die Mundschleimhaut aufgenommen werden.
Bei Sublingualtabletten ist es tatsächlich so, dass die Wirkung schneller eintritt und stärker ist als bei anderen Darreichungsformen (des selben Wirkstoffs in derselben Dosis) wie Filmtabletten oder Kapseln. Das liegt daran, dass es sich hierbei um eine parenterale Verabreichung handelt, d.h. der Wirkstoff gelangt direkt in den systemischen Blutkreislauf und muss nicht erst den Magen-Darm-Trakt und die Leber durchqueren, was einerseits dauert und wo oft Teile des Wirkstoffs bereits inaktiviert werden.
Es bringt aber zum Beispiel nichts, sich eine Ibu unter die Zunge zu legen. Ibuprofen liegt in "harten" Filmtabletten vor und löst sich im Speichel gar nicht erst auf. Filmtabletten sind so konstruiert, dass sich sich genau im Darm auflösen und dort den Wirkstoff freisetzen.
Ich wünsche dir alles Gute.
Man kann sie gleichzeitig einnehmen.
Üblicherweise ist das Dosierschema für Aripiprazol aber 1-0-0, d.h. mit morgendlicher Einnahme, weil es in manchen Fällen aktivierend wirken und dadurch bei abendlicher Einnahme Schlafstörungen hervorrufen kann.
Für die Wirkung ist der Einnahmezeitpunkt aber irrelevant, solange er täglich gleich bleibt.
Ich wünsche dir alles Gute.
Ein paar hundert Milligramm. Davon sind 10 mg der Wirkstoff Dexamfetamin.
Ja, denn alle Aspirin-Präparate enthalten den Wirkstoff Acetylsalicylsäure (ASS) und ASS wirkt blutverdünnend.
Das heißt, nicht nur alle Aspirin-Präparate, sondern allgemeiner alle Präparate, die ASS enthalten, wirken blutverdünnend. Das betrifft also zum Beispiel auch Thomapyrin, ASS-ratiopharm, ASS STADA, etc.
Ich wünsche dir alles Gute.
Das hängt von der Darreichungsform des Medikaments ab. Die Wirkung zeigt sich nur schneller, wenn der Wirkstoff tatsächlich über die Mundschleimhaut aufgenommen wird. Das ist nicht bei allen Darreichungsformen der Fall.
Was du suchst, sind sog. Sublingualtabletten. Diese können ohne Wasser eingenommen werden, indem sie unter die Zunge gelegt werden, wo sie sich schnell auflösen und anschließend über die Mundschleimhaut resorbiert werden.
Das ist bei normalen Tabletten oder Filmtabletten nicht der Fall. Sie haben eine festere Konsistenz als Sublingualtabletten und zerfallen beim Kontakt mit Speichel nicht, sondern bleiben ganz. Zersetzen kann eine solche Tablette nur der Magen und der Darm - und das sind auch die Orte im Körper, an denen Tabletten und Filmtabletten aufgenommen werden.
Du musst also nur auf die Verpackung deines Medikaments gucken. In der Regel ist dort die Darreichungsform angegeben, etwa "Tabletten", "Filmtabletten", "Kapseln" oder eben "Sublingualtabletten". Handelt es sich um Letzteres, sind sie für eine wie von dir beschriebene Einnahme gedacht und werden auch korrekt aufgenommen. In allen anderen Fällen führt ein unter die Zunge legen nicht zum Erfolg.
Ich wünsche dir alles Gute.
Vorab ein Wort zur Vorsicht: Benzodiazepine machen bei längerer Einnahme schwer abhängig. Das Risiko ist bei einmaliger Einnahme für einen Flug zwar nicht hoch, dennoch sollte man zuvor alle anderen Mittel ausprobieren, bevor man zum hochriskanten (wenn auch hochwirksamen) Mittel der Benzodiazepine greift.
Grundsätzlich sind sowohl Alprazolam, als auch Bromazepam Benzodiazepine, bei denen die anxiolytische (angstlösende) Wirkung im Vordergrund steht. Von der Wirkung her eignen sich also beide gut gegen Angsterkrankungen. Aber wie sieht es mit Wirkungseintritt und Wirkdauer aus?
Zur PharmakologieDie wesentlichen pharmakologischen Parameter sind in diesem Fall Tmax und T1/2:
- Tmax: Dauer bis zur maximalen Plasmakonzentration (= bis zur maximalen Wirkung)
- T1/2: Dauer ab Tmax, bis der Stoff vom Körper wieder zur Hälfte abgebaut wurde
Tmax liefert ein Maß dafür, wie schnell ein Medikament wirkt, T1/2 dafür, wie lange ein Medikament wirkt. Beides hängt natürlich noch von etlichen anderen Faktoren (v.a. der Dosis-Wirkungs-Kurve) ab, aber Tmax und T1/2 geben zumindest eine erste Idee dafür und das soll uns in diesem Rahmen genügen.
Für Alprazolam und Bromazepam kann man diese Werte aus Benzodiazepin-Äquivalenztabellen ablesen, die man zahlreich in der Literatur oder im Web findet, zum Beispiel hier.
Dort wird angegeben:
- Alprazolam: Tmax = 1-2h, T1/2 = 12-15h
- Bromazepam: Tmax = 1-2h, T1/2 = 15-28h
Das suggeriert: Alprazolam und Bromazepam wirken gleich schnell, aber Alprazolam wird etwas schneller abgebaut, d.h. Bromazepam wirkt etwas länger. Die klinische Erfahrung zeigt aber, dass sich auch die Wirkdauer beider Wirkstoffe nicht wirklich unterscheidet und sowohl bei Alprazolam, als auch bei Bromazepam typischerweise 8-12h beträgt. Das ist vereinfacht dadurch zu erklären, dass sich die Dosis-Wirkungs-Kurven von Alprazolam und Bromazepam unterscheiden und die Dosis-Wirkungs-Kurve von Bromazepam die längere Halbwertszeit wieder wett macht.
Das FazitAlprazolam wirken (bei vergleichbaren körperlichen Eigenschaften) in der Regel in etwa gleich schnell und in etwa gleich lang wie Bromazepam. Da auch die Wirkung (vorrangig anxiolytisch) bei beiden vergleichbar sind, eignen sich beide Wirkstoffe gut gegen krankhafte Flugangst, vorbehaltlich individueller Unterschiede, die es natürlich immer geben kann.
Abschließend noch ein Wort zur Dosierung: Die Äquivalenztabelle oben listet auch die Äquivalenzdosen. Danach entsprechen 1,5 mg Alprazolam etwa 6 mg Bromazepam - oder umgerechnet: 1 mg Alprazolam entspricht etwa 4 mg Bromazepam. Um eine vergleichbare Wirkung zu erhalten, muss man Alprazolam also im Verhältnis 1:4 zu Bromazepam dosieren. "Gleiche Wirkung = Gleiche Dosis" gilt nicht (wie nie in der Pharmakologie).
Ich wünsche dir alles Gute.