Suche eine Funktion mit unendlich vielen Hochpunkten, die alle unterschiedliche Abstände haben?
Hallo,
ich hatte da natürlich sofort an einen Sinusfunktion gedacht. Ich weiß allerding nicht ob man hier den Abstand zwischen den Extrempunkten immer wieder in einer Funktion ändern kann ?
Habt ihr da eine Idee?
Hier nochmal die Aufgabe
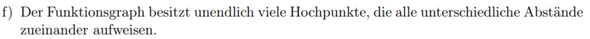
Über eine Rückmeldung würde ich mich freuen :)
Grüße
Hier sind die anderen Aufgaben.

3 Antworten
Die Idee mit dem Sinus ist schon Mal gut. Du müsstest jetzt nur irgendwas damit machen, damit die Abstände sich verändern. Tipp: welcher Parameter von der allgemeinen Sinusfunktion verändert den Abstand der Hochpunkte? Wie wäre es, wenn du dafür sorgst, dass sich dieser Parameter mit der Zeit ändert?
indem Du diesen z. B. mit der "Laufvariablen" x gleichsetzt (oder als Bruchteil von x, um den Graphen weiter "auseinanderzuziehen")
Du kannst den Parameter durch eine Funktion ersetzen, die von x abhängt.
Zum Beispiel kann man b mit x ersetzen. (Das ist ein Beispiel welches aber nicht erfüllt, da die Funktion bdann symmetrisch ist. Du musst ein wenig rumprobieren)
Wie stellt man (beweisbar) sicher, dass die Abstände paarweise verschieden sind?
Gute Frage, ich dachte, dass nur gemeint war, dass die benachbarten Abstände unterschiedlich sein sollen, so ist es natürlich etwas komplizierter. Spontan fällt mir gerade nichts ein
Also die anderen Aufgaben sehen ja ziemlich einfach aus, es würde also denke ich einfach nur ungenau formuliert.
Man kann versuchen, den Sinus zu skalieren, etwa so
x^2 sin( Pi x)
Gelöscht.
Ach - die Antwort war Mist, weil ich mir selbst widersprochen habe. Ich fasel was von "asymmetrisch" und schreib x² hin. Manchmal sollte ich besser 2x denken.
Also bei der allgemeinen Sinusfunktion wäre es der Faktor b.
f(x) = a*sin(b*x+c) + d
Wie sorge ich dafür das sich der parameter mit der zeit ändert?