Mathe Hilfe?
Kann mir jemand bei Aufgabe 1 helfen ?

2 Antworten
sie muss 3. Grades sein, damit sie zwei Extrem- und einen Wendepunkt hat
in den Übergangspunkten müssen die Funktionswerte und die Ableitungen gleich sein
wenn f die gesuchte Funktion ist dann muss gelten:
f(0)=0
f'(0)=0
f(2)=4
f'(2)=0
3a)
ausmultiplizieren, ableiten und Ableitung nullsetzen
doppelte Nullstelle bei 0 und jeweils Nullstelle mit Vorzeichenwechsel bei 1 und 2
Flächenstücke von 0 bis 1 und von 1 bis 2, das sind auch die Integrationsgrenzen. Das Stück zwischen 1 und 2 liegt unterhalb der x-Achse, hier ist der Flächeninhalt der Betrag des Integrals
Alles richtig nur wird nach dem Integral nicht gefragt das ist eine Klasse höher
die gesuchte Fläche muss mit dem Integral berechnet werden, falls GTR oder CAS verwendet werden, vielleicht auch mit diesen
Mag sein aber ich sehe in aufgabe 3 keine frage stellung zum integral im minus bereich
Jap absolut nur die information zu unterhalb war nicht an der fragestellung orientiert
Ich komme bei 3a irgendie nicht weiter. ich habe die durch 2 geteilte Ableitung gebildet, die lautet 3xhoch2 - 6x + 2, aber damit kann ich ja nicht die pq formel machen
kurze frage warum solltest du diese formel einklammern das ergibt keinen Sinn
Du verstehst es nicht oder?`Es geht darum das man die formel nicht teilt sondern umformt bis man sie ableitet um fehler zu vermeiden
die ausmultiplizierte Form lautet f(x)=x⁴-3x³+2x²
diese zweimal ableiten, dann zeigen: f'(0)=0 und f''(0)>0 wenn das stimmt, dann hat man bei x=0 einen Tiefpunkt
Es ergeben sich 4 Bedingungen:
Damit wird mit der Lösung des aus dem Ansatz "ganzrationale Funktion 3. Grades" entstehenden LGS
Skizze:

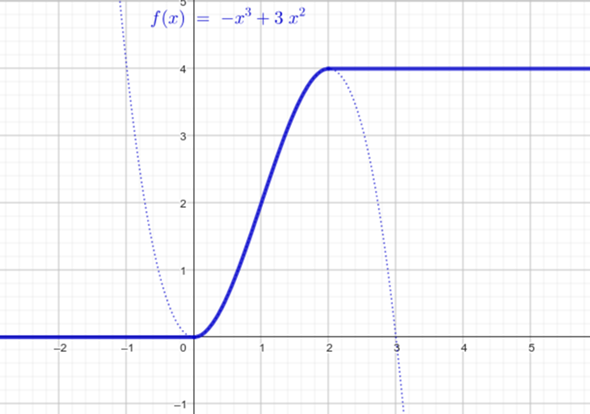
Danke! hast du auch Nummer 3?
Super danke, direkt verstanden. Hast du vielleicht auch Nummer 3? 2 konnte ich gut bearbeiten