Könnt ihr mir helfen, bei meiner Mathewette?
Ich habe von einem Arbeitskollegen eine Challenge bekommen. Er meinte, dass er noch nie eine Person getroffen hat, welche diese Aufgabe geschafft hat. Er meinte außerdem, dass diese Aufgabe nicht mit einfachen Ausprobieren funktioniert, sondern mit Logik. Leider hab ich bisher wirklich keine Ahnung, wie ich an diese ganze Sache herangehen soll. Haben irgendwelche Mathegenies eventuell bereits eine Lösung?
Die Aufgabe:
Gesucht wird EINE neunstellige Zahl, bestehend aus den Ziffern 123456789.
Keine Ziffer darf doppelt stehen, alle müssen vorhanden sein und die Zahl darf nicht verändert werden. Es ist auch keine Kommazahl.
Jetzt kommt der Haken. Jede Zahl muss (etwa so) Teilbar sein.
X X X X X X X X X
:2__I
:3____I
:4______I
:5________I
:6__________I
:7____________I
:8______________I
:9________________I
Ich hoffe Ihr versteht die Aufgabe und könnt mir helfen!
LG.
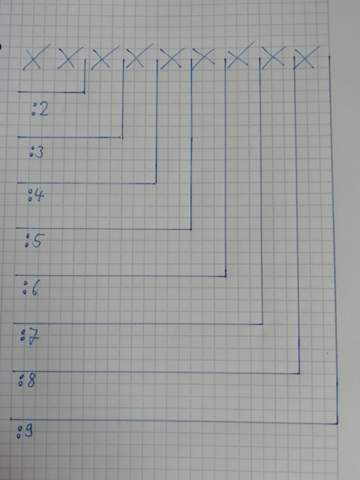
Irgendwie gab es einen Fehler, als ich die Aufgabe reingestellt habe. So könnt Ihr euch das sicherlich besser Vorstellen.
Jetzt hast Du die Frage geändert und die | bis auf einen gelöscht. Was soll das JETZT bedeuten?
Ich habe ein Bild reingestellt, was es hoffentlich etwas verständlicher macht.
Was meinst du mit den "_____|"? Soll die Zahl durch 2 und durch 3 und ... teilbar sein? Oder durch irgebdeine Zahl, die mit 2 anfängt?
Die ersten Zwei Zahlen müssen durch 2 teilbar sein. Die ersten Drei Zahlen müssen durch 3 teilbar sein. Die ersten Vier Zahlen dann durch 4 und so weiter.
4 Antworten
Ich denke mal, dass 381654729 gesucht ist, wenn ich richtig verstanden habe, wie du (bzw. dein Kollege) das mit der Teilbarkeit gemeint hast...
- 38 ist durch 2 teilbar.
- 381 ist durch 3 teilbar.
- 3816 ist durch 4 teilbar.
- 38165 ist durch 5 teilbar.
- 381654 ist durch 6 teilbar.
- 3816547 ist durch 7 teilbar.
- 38165472 ist durch 8 teilbar.
- 381654729 ist durch 9 teilbar.
Ich habe die Zahl einfach mit Ausprobieren gefunden, da ich zu faul gewesen bin da extra darüber nachzudenken. Dazu habe ich ein kleines Python-Programm geschrieben, welches mir dann die Zahl 381654729 als Ergebnis ausgegeben hat.
from itertools import permutations
for p in permutations("123456789"):
s = "".join(p)
passt = True
for m in range(2, 10):
if int(s[:m]) % m != 0:
passt = False
break
if passt:
print(s)
[Die Laufzeit des Programms beträgt bei mir etwa 0,3 Sekunden. Und das Programm zu schreiben hat auch nicht lange gedauert.]
Ich habe inzwischen auch mal einen Lösungsweg ohne dieses Programm aufgeschrieben...
https://www.dropbox.com/s/h00f2hnmuv9t67t/Teilbarkeit381654729.pdf?dl=0
0.0 okay das hat mich sehr überrascht. Er meinte, dass er dafür 2 Stunden gebraucht hätte, um die Lösung(natürlich nur mit dem Kopf) herauszufinden.
Das ist genau die richtige Weise, wie ich die Teilbarkeit gemeint hatte.
Vielen Dank!
Spontan:
Die fünfte Stelle ist schon mal ein 5
die 2., 4., 6., 8. Stelle sind aus 2, 4, 6, 8, also gerade, der Rest aus 1, 3, 5, 7, 9
...
Schau mal, was Dir sonst noch auffält.
Sagen wir mal, ganz willkürlich, dass die erste Ziffer eine 2 ist, dann 3, dann 4, dann 7, dann 5. Die ersten 5 Ziffern, wären also die Zahl 23.475. Diese müsste dann um 5 teilbar sein. Wenn danach noch eine Zahl dazu kommt, sagen wir mal eine 6, müsste dann die Zahl 234.756 durch 6 teilbar sein. Das ist so das schwierige an dieser Aufgabe.
Hallo, die Lösung lautet 381654729 weil:
38:2=19
381:3= 127
3816:4=954
38165:5=7633
381654:6=63609
3816547:7=545221
38165472:8=4770684
381654729:9=42406081
Ich hoffe, dass ich dir helfen konnte.
Liebe Grüsse Amélie
So kannst du Lösung im Kopf ohne Computer finden (dazu musst du aber die Teilbarkeitsregeln kennen):
- Wenn eine Zahl durch 5 teilbar ist, endet sie auf 0 oder 5, d.h. die 5te Ziffer ist eine 5.
- Wenn eine Zahl durch 2, 4, 6 oder 8 teilbar ist, dann ist sie gerade. Eine Zahl ist genau dann gerade, wenn sie auf 0, 2, 4, 6 oder 8 enden. Also müssen die zweite, vierte, sechste und achte Ziffern aus 2, 4, 6, 8 bestehen. Die Ziffern sind also abwechselnd gerade und ungerade.
- Wenn eine Zahl durch 4 teilbar ist, dann sind ihre letzten beiden Ziffern x0, x4, x8 für eine gerade Ziffer x oder y2, y6 für eine ungerade Ziffer y. Da bei uns die Ziffern abwechselnd gerade und ungerade sind, muss also die 4te Ziffer und die 8te Ziffer eine 2 oder 6 sein. (durch 8 teilbar bedeutet insbesondere durch 4 teilbar) Das heißt, dass die 4 und 8 für die 2te und 6te Ziffer übrig sind.
- Wenn eine Zahl durch 3, 6 oder 9 teilbar ist, ist sie insbesondere durch 3 teilbar. Eine Zahl ist genau dann durch 3 teilbar, wenn ihre Quersumme (also die Summe ihrer Ziffern) durch 3 teilbar ist. Das bedeutet, dass die Summe der ersten 3, 6 und 9 Ziffern jeweils durch 3 teilbar ist. Wenn ich zwei durch 3 teilbare Zahlen voneinander subtrahiere kommt eine durch 3 teilbare Zahl raus, also ist
1.Ziffer + ... +6.Ziffer - (1.Ziffer + 2.Ziffer+ 3.Ziffer) = 4.Ziffer + 5.Ziffer + 6.Ziffer
durch 3 teilbar. Wir wissen bereits, dass
4te Ziffer = 2 oder 6,
5te Ziffer = 5
6te Ziffer = 4 oder 8.
Probiert man die 4 Möglichkeiten durch, sieht man, dass nur
1) □4□258□6□ und
2) □8□654□2□
funktionieren.
Die 1te und 3te Ziffer sind ungerade, aber nicht 5, also 1, 3, 7 oder 9. Damit die Summe der ersten 3 Ziffern durch 3 teilbar ist, müssen diese beiden Ziffern
im Fall 1) 1 und 7 sein,
im Fall 2) 1 und 3/ 1 und 9/7 und 3/7 und 9 sein.
- Wenn eine Zahl durch 8 teilbar ist, dann sind ihre letzten 3 Stellen durch 8 teilbar. Für die 7te Ziffer bleibt im Fall 1) nur 3 oder 9 übrig. In diesem Fall wären die letzten 3 Stellen der letzten 8 Stellen also 836 oder 896. Davon ist nur 896 durch 8 teilbar, also sind die möglichen Lösungen in Fall 1)
147258963 und 741258963.
Im Fall 2) kann die 7te Ziffer gleich 1, 3, 7 oder 9 sein. In diesem Fall wären die letzten 3 Stellen der letzten 8 Stellen also 412, 432, 472 oder 492. Davon sind nur 432 und 472 durch 8 teilbar, also sind die möglichen Lösungen in Fall 2)
183654729, 381654729, 189654327, 189654723, 981654327, 981654723, 789654321 und 987654321.
- Nun prüfen wir bei allen diesen möglichen Lösungen nach, ob ihre ersten 7 Stellen durch 7 teilbar sind. Das stimmt nur für
381654729.
Das ist also die einzige Lösung!
Ich hoffe, das ist verständlich. Sag bescheid, wenn ich bestimmte Stellen genauer erklären soll. Ich habe an keiner Stelle einfach geraten oder so!