Kann mir jemand helfen die Aufgaben zum Thema "Satz des Pythagoras" zu verstehen?



Ich habe kein Plan, wie ich bei den Aufgaben vorgehen soll. Satz des Pythagoras lautet: c^2 = a^2 + b^2. Als ich die erste Aufgabe gelöst habe, bin ich auf ein Verhältnis von 4:3 gekommen. Ob das so stimmt, weis ich nicht. Ich wäre froh, jemand sich Zeit nimm und mir die Aufgaben erklären kann. Ich möchte keine direkte gratis Lösung. Nur wie ich vorgehen soll. Ich möchte die Aufgaben schon irgendwie dann selber lösen. Vielen Dank :).
3 Antworten
Bei Aufgabe 1 verstehe ich ehrlich gesagt nicht mal, was gefragt ist. Es gibt kein Sechseck und die eingezeichneten Seiten sind gleich lang, weil sie die Seiten eines gleichseitigen Dreiecks bzw. die Kanten eines Oktaeders sind, die per Definition gleich lang sind.
Bei 2 ist die Seitenlänge des Sechsecks √(4²+4²) = √32. Das heißt, die Fläche ist 8*√3 ≈ 13,856cm².
Bei 3 ist die Höhe √(5²+5²) = √50 und für die Breite und Tiefe gilt, dass die √50 die Diagonale ist, das heißt, die Seitenlängen sind jeweils 5 cm. Daraus ergibt sich eine Oberfläche von 2*5² + 4*5*√50 ≈ 191,421cm²
Bei 4 ist die Kantenlänge √(12²+12²) = √288 und die Oberfläche dadurch √3 * 288 ≈ 498,831cm²
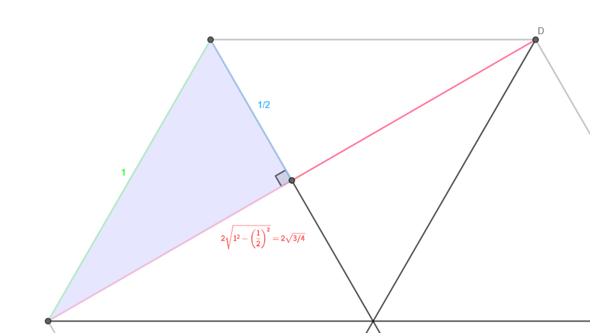
PS: Nachtrag zu Aufgabe 1: Ich hab jetzt erst gesehen, dass das keine dreidimensionale Projektion eines Oktaeders ist, sondern einfach ein Sechseck mit einem Dreieck drin. Hamburger02 hat schon gut erklärt, wie man das berechnet. Bei ihm hat s2 die Länge 3 und s1 die Länge √3, wodurch das Verhältnis √3/3 rauskommt. Ich hätte es etwas anders geometrisch aufgebaut, so dass s1 die Länge 1 hat. Dann kannst du ein rechtwinkliges Dreieck konstruieren, bei dem die Hypotenuse die Länge 1 hat und eine der Katheten die Länge 1/2. Daraus ergibt sich, dass die Hälfte von s2 = √(3/4) ist und das Verhältnis von s1 und s2 ist 1/2√(3/4). Das Ergebnis sieht auf den ersten Blick ganz anders aus, als das Ergebnis von Hamburger02, aber wenn du beide Terme mit dem Taschenrechner berechnest, siehst du, dass bei beiden das selbe Ergebnis rauskommt. Etwa 0,577

Nicht immer hilft nur der Pythagoras. Bei der Aufgabe 2 z.B. kannst du die Länge der Quadratseite des Quaders mit Hilfe des Strahlensatzes bekommen, es ist 10:5 = 10:x, d.h. die Quadratseitenlänge beträgt 5. Ähnlich kannst du wahrscheinlich auch die Höhe des Quaders und damit dann auch seine Oberfläche bestimmen.
Bei der 4 kannst du mit HIlfe des Pythagoras die Länge der Tetrahederseiten bestimmen und damit leicht die Oberfläche. Es handelt sich bei den Seiten des Thetraheders um gleichseitige Dreiecke, deren Fläche nur von der Seitenlänge abhängt.
Wie hast du die 1 gerechnet?
Ich habe kein Plan, wie ich bei den Aufgaben vorgehen soll.
Zu allererst muss man einen rechten Winkel suchen und wenn es den nicht gibt, muss man sich eben selber einen machen. Ohne rechtwinkliges Dreieck geht der Pythagoras nicht. Sobald man ein passendes rechtwinkliges Dreieck gefunden hat, ist der Rest nur noch Handwerk.
Aufgabe 1:
Da gibts noch keinen rechten Winkel, also machen wir uns selber einen:

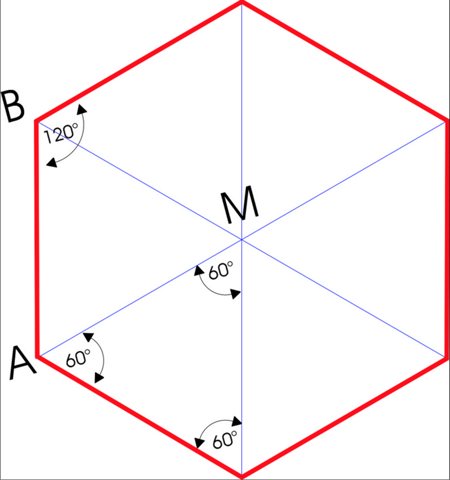
Um die Winkel zu benennen, muss man einige Eigenschaften eines Sechsecks kennen. Die braucht man auch für die weiteren Aufgaben:

Ein Sechseck besteht aus 6 gleichseitigen Dreiecken und alle Winkel sind entweder 60° oder 120°.
Zurück zur Aufgabe:
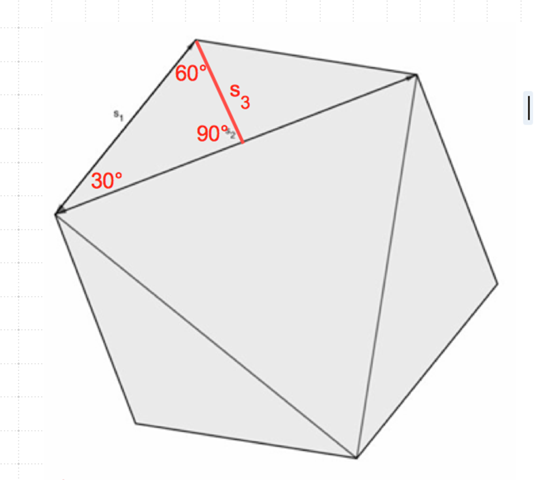
Aus den bekannten Winkeln können wir nun s3 berechnen:
sin 30° = s3 / s1
s3 = s1 * sin 30° = 1/2 * s1
Nun haben wir alle drei Seiten und können das Verhältnis bilden:
s1 / s2
s2 müssen wir ersetzen und das kriegen wir über den Pythagoras raus:
s1^2 = (s2/2)^2 + s3^2
(s2/2)^2 = s1^2 - s3^2 = s1^2 - (s1/2)^2
da ziehen wir die 1/2 jeweils vor die Klammer:
1/4 * s2^2 = s1^2 - 1/4 s1^2
1/4 * s2^2 = 3/4 s1^2
s2^2 = 3 s1^2
s2 = √3 s1^2 = s1 * √3
Nun können wir s2 im Verhältnis austauschen:
s1 / s2 = s1 / s1 * √3 = 1/√3 = √3 / 3
Probe: wenn man die Strecken s1 und s2 misst und das Verhältnis bildet, kommt in etwa 0,57 raus. Das ist auch das Ergebnis, wenn man √3 / 3 ausrechnet. Also stimmt das.
Alles richtig, aber ein Hinweis: Zur Berechnung von s3 ist der Sinus ein unnötiger Umweg, man kann das direkt aus den Eigenschaften des gleichseitigen Dreiecks ableiten.