Kann man die fehlende Seite berechnen?
Die obere und untere seite sind nicht parallel

3 Antworten
Edit: Direkt lösbar mit den angegebenen Zahlen ist es eigentlich nur, wenn die beiden Geraden parallel sind. Dann wäre das die Lösung:
27.1+15 x cos(alpha)
Wenn die nicht parallel sind, dann kannst Du die gesuchte Länge als Funktion ausdrücken. Diese ist eine Funktion, die eine weitere Größe der gesuchten Länge zuordnet. Eine weitere Größe, das kann eine weitere Seite sein oder ein weiterer Winkel außer Alpha und dem rechten Winkel rechts unten sein.
Fazit, Du verschweigst uns etwas, oder die Funktion ist gesucht, oder Du hast vergessen, etwas abzuschreiben. In Deiner Zeichnung sind ja die oberen und die unteren Seiten parallel, Dein Viereck ist also ein so genanntes Trapez. Das sind Vierecke, bei denen 2 Seiten parallel sind.
Achtung! Da steht die beide parallel aussehenden Seiten sind NICHT parallel.
Damit stimmt dein Ansatz nicht.
Wenn die beiden Seiten nicht parallel sind, ist das Viereck ohne weitere Angaben weder konstruierbar noch berechenbar.
Ich war arbeiten und bin eben erst wiedergekommen. Vor der Arbeit hatte ich kaum Zeit, mir die Sache genauer anzusehen.
Ok danke. das geht, obwohl oben rechts kein rechter winkel ist?
Nicht direkt. Du mußt noch die fehlenden Winkel berechnen und oben eine Hilfslinie ziehen, die parallel zur unteren Grundseite ist. Deren Länge addierst Du dann zum über den Kosinus ermittelten Wert.
Wenn der Winkel oben rechts nicht bekannt ist, dann muss entweder die Länge der Strecke rechts bekannt sein, oder die Lösung ist nicht bestimmt, weil sie ja davon abhängt, wie die 27.10-Strecke „liegt“. Ich bin davon ausgegangen, dass die beiden horizontalen Seiten parallel sind. Wenn sie es sind, folgt daraus dass der Winkel rechts oben ein rechter Winkel ist. Wenn die Seiten aber nicht parallel ist, dann ist die Lösung nicht bestimmt. Dann gibt es eine Lösungsmenge, je nach dem wie die obere Seite zur unteren Seite steht.
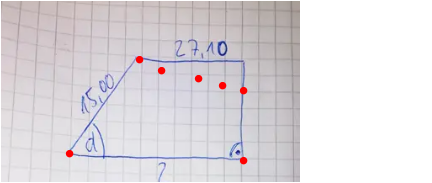
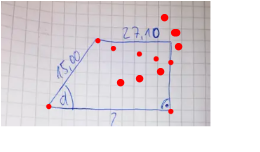
so sieht das Viereck wirklich aus

nun die 27.10 als Kreisbogen

man kann auf die untere Seite unendlich viele Senkrechte zeichnen , die die Bogen teilen
Ergo : nicht lösbar
Nur, wenn man den Winkel ß oben rechts kennt. Dann kann man nämlich damit, mit einer zur unteren Seite Parallelen Strecke sowie einem Teil der Gegenkathete von Alpha ein weiteres rechtwinkliges Dreieck erstellen und mit cos(ß) die Länge des rechten Teil der unteren Seite errechnen.
27,1 ist die Länge der oberen Seite; die ist aber nicht parallel zur Grundseite unten.