Fläche unter einer Funktion berechnen?
Hallo, ich habe folgende Matheaufgabe vorliegen:

Jetzt habe ich leider keine Ahnung wie ich diese lösen soll, weil ich in der letzten Mathestunde nicht anwesend war. Das ist das Kapitel Anwendungen der Integralrechnung.
Wie genau gehe ich hier vor? Wie berechne ich es mit Integration und was bedeutet es überhaupt, etwas elementar zu lösen?
Ist das bei Integration dann einfach ein bestimmter Integral mit den Grenzen -3 und 3?
Ich hoffe ihr könnt mir helfen.
3 Antworten
Integralrechnung anwenden!
Die Grenzen F(3) - F(-3) einsetzen in die Stammfunktion bzw. Flächeninhaltsfunktion und ausrechnen!
Die Funktion kannst du aus der Grafik aufstellen!
Bei b musst du schrittweise vorgehen!
Elementar bedeutet durch Zerlegung in Figuren nehme ich an. Beziehungsweise Ober- und Untersummen!
VG
Klar! Fie Grafen aus dem Koordinatensystem!
a) ist eine lineare Funktion y=mx+n!!!
b) musst du wohl zerlegen
c) lineare Funktion
Ahh vielen Dank, ich glaube jetzt hab ichs verstanden. Vielen Vielen Dank!
Du musst schon die Geradengleichungen der Begrenzungen heranziehen. Im ersten Fall ist die rote Linie durch die Funktion f(x)=3-x darstellbar (integrieren dann über den Bereich 0 bis 3), im zweiten Fall musst Du abschnittsweise drei verschiedene Funtionen heranziehen; die Integration ist dann auch entsprechend abschnittsweise zu machen usw.
Was hier mit "elementar" gemeint ist, ist selbst einem Mathematikprofessor nicht wirklich klar bzw. nicht eindeutig genug. Ich vermute mal, dass hier eine geometrische Lösung gegenübergestellt werden soll, also die Hälfte eines 3x3 Quadrats im ersten Fall, also 1/2*(3*3), im zweiten Fall dann 1/2*(2*3)+(1*3)+1/2*(1*3) und in letzten Fall dann 1/2*(6*2)+(6*2)
Elementar heißt: die Fläche mit Mitteln der Geometrie zu berechnen.
Das Dreieck a) ist rechtwinklig, hat also die Flächenformel A = ab/2.
Demnach ist A = 3 * 3/2 = 4,5 F.E.
Integriert: Die Funktion ist f(x) = -1/2 x + 3.
∫(-x/2 + 3(dx = 1/2 * x²/2 + 3x
von 0 bis 3
Integration ist ja klar, oder?
Pardon: f(x) = -x + 3
Daher ∫(-x + 3)dx = -x²/2 + 3x von 0 bis 3
Hatte mich vertippt.
Lösungsvorschlag z.B.
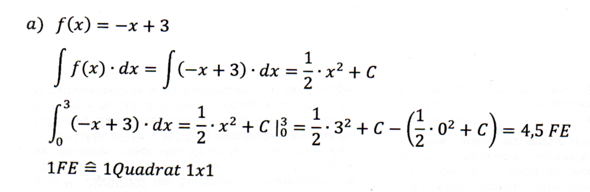
Gruß, H.
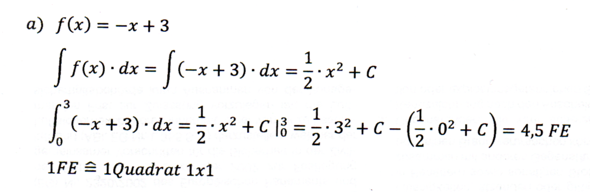
Danke, aber was genau muss ich integrieren? Ich muss ja irgendeine Formel integrieren, also z.B. bei einer quadratischen Funktion müsste ich ja dann x^2 integrieren. Aber hier habe ich nichts gegeben?