Mathe Integralrechnung!?
Berechne den Flächeninhalt der Fläche zwischen den Graphen von f(x)=x^4-9x^2 und der x-Achse im Intervall [-2;4]
als erstes hab ich nullstellen berechnet da kam 3 und -3 raus
danach hab ich ins integral gesetzt
integral(-2bis4) x^4-9x^2= -4,8
ist das richtig?
flächeninhalt kann ja nicht negativ sein
2 Antworten
Eine Nullstelle mit Vorzeichenwechsel muss immer als Intervallgrenze der Teilintegrale verwendet werden. Du kannst hier also nicht direkt von -2 bis 4 integrieren, da eine Teilfläche unterhalb, die andere oberhalb der x-Achse liegt.
Bei 3 gibts eine Nullstelle mit Vorzeichenwechsel, diese Nullstelle teilt die zu berechnende Fläche
Zwischen -2 und 3 ist die Fläche negativ. Diese kann mit einem Integral berechnet werden. Das Ergebnis muss positiv sein (also Betrag davon nehmen). Zwischen 3 und 4 ist die Fläche positiv. Diese Teilfläche muss getrennt berechnet werden und zum Betrag der anderen Teilfläche addiert werden
hier die Lösung:
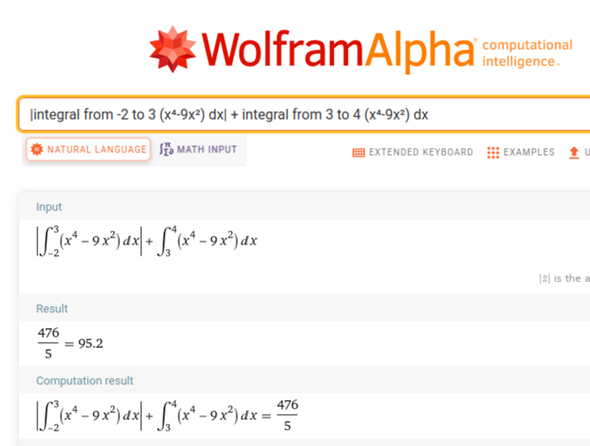
oder mit Betrag der Funktion:
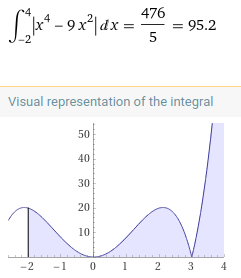
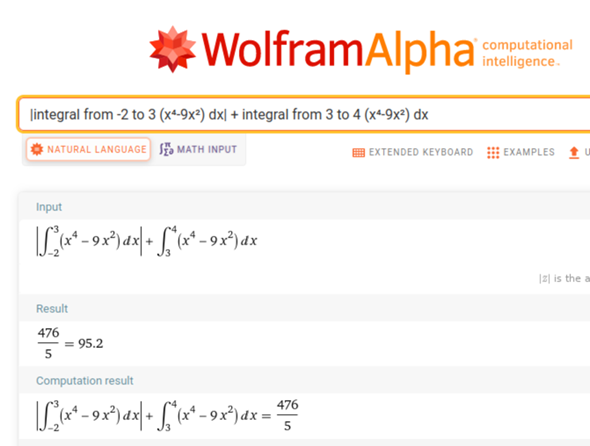
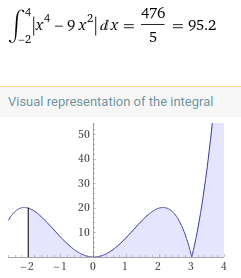
wenn du die Fläche ausrechnen möchtest, müssen alle Teilfächen positiv sein. Liegt die Fläche unterhalb der x-Achse und ist das Integral negativ, dann wird bei der Fläche das Minus weg gelassen
also ein Flächeninhalt kann nicht negativ sein aber anhand ihrer Lösung kommt was positiv raus aber bei mir nicht
Wenn Du nur die Beträge addierst, die ja grundsätzlich ü,positiv sind, kann nur etwas Positives herauskommen.
Hallo,
Du hast die Nullstelle bei x=0 vergessen. Du mußt getrennt integrieren:
Von -2 bis 0, von 0 bis 3 und von 3 bis 4, danach die Beträge der Flächen addieren. Tust Du das nicht, verrechnest Du Flächen unter und über der x-Achse und bekommst ein falsches Ergebnis.
Herzliche Grüße,
Willy
Ich habe jetzt drei integrale aufgestellt diese ausgerechnet und danach alle + genommen und hab als Ergebnis -4,8 raus