Integralrechnung vs. Flächeninhalt?
Hallo :-)
Ich hatte eine grundsätzliche Frage zu diesem Thema.
Wir haben im Matheunterricht (siehe Fotos) diese Themen behandelt.
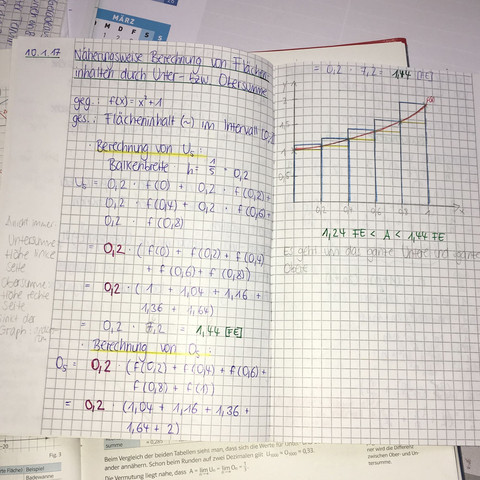
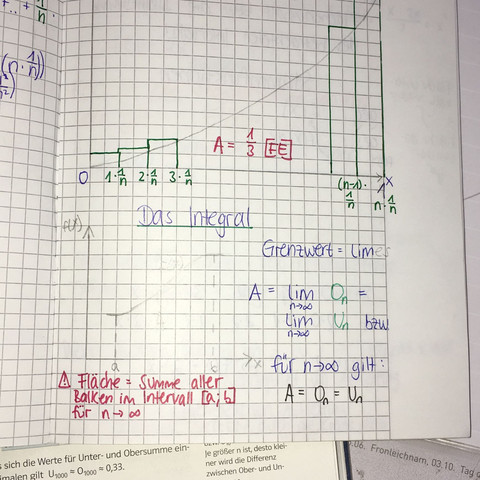
Nun verstehe ich nicht, welchen Zusammenhang die "Bedeutung von Flächeninhalten" & die "Ober/Untersumme" mit dem Integral hat.
1-Die Bedeutung von Flächeninhalten berechnet die Gesamtänderung am Ende. Aber wie macht das das Integral? Wo zieht er die Werte, die bei der Berechnung der Fläche unterhalb der x-Achse rauskommen, ab?
2-Ist das Integral auch die Fläche, wenn die Funktion positiv ist, sprich der Graph verläuft nicht unterhalb der x-Achse?
Denn dann könnte ich mir erklären, warum die Ober/Untersumme als FLÄCHENINHALT im Kapitel des Integrals zusammengefasst wurde.
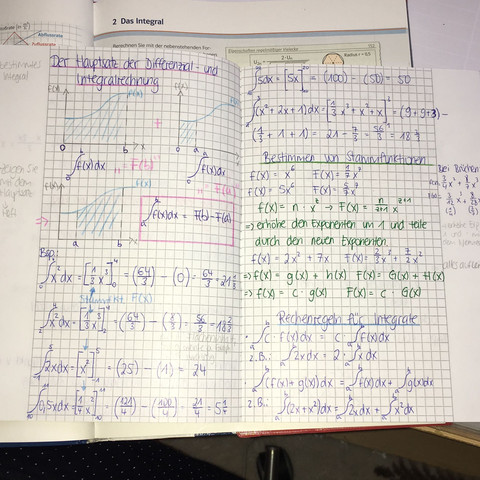
3- Was ist die Funktion des Hauptsatzes? Dass man die Fläche in einem Intervall berechnen kann?
4- Die Aufgabe mit der Solarenergie (Siehe Fotos) : Nr.1- ist da nun der Flächeninhalt oder das Integral gefragt?





2 Antworten
Das Intregralzeichen ist bereits ein stilisiertes "S" welches für Summe steht. Bei dem Integral werden die infinitesimal kleinen Flächeneimheiten unter der Kurve aufsummiert was dann die Fläche ergibt. Grüße Technoir
Der Hauptsatz beschreibt den Zusammenhang zwischen der Aufleitung einer Funktion und ihrem Integral. Die ersten beiden Fragen versteh ich nicht wirklich.