Integral und Flächeninhalt?
Hallo Leute,
weiss jemand zufällig wie die Aufgabe 2. funktioniert und kann mir erklären wie ich vorgehen muss? Auf jeden fall soll das mit der Ober- und Untersumme gelöst werden.
Ich danke schonmal im Voraus für hilfreiche Antworten!
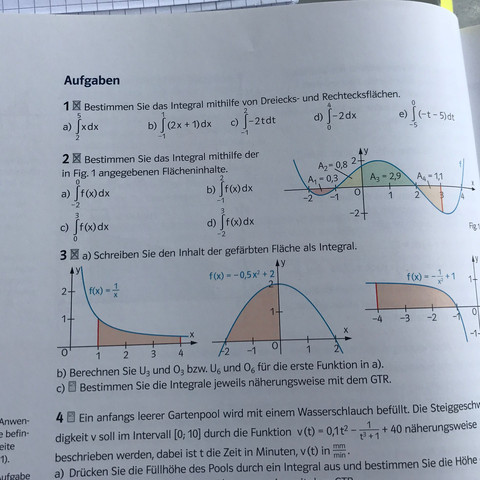
2 Antworten
Aufgrund der Nullstellen ist
f(x) = a(x+2)(x+1)(x-2)(x-4) | ausmultiplizieren
f(x) = a(x⁴ -3x³ - 8x² + 12x + 16) | integrieren
Ⅰ = ∫ f(x)dx
Ⅰ = a (x⁵/5 - 3x⁴/4 - 8x³/3 +6x² + 16x
Wenn ich die Teilfläche A₃ = 2,9 auswähle, ist es das Ⅰ von 0 bis 2.
Das bedeutet, ich kann die untere Grenze vernachlässigen, sie ist gleich Null.
2 in Ⅰ eingesetzt, ergibt a * 436/15 = 2,9
a = 0,01 gerundet
Eine schnelle Prüfung für a = 0,01 ergibt tatsächlich die Nullstellen
x = {-2; -1; 2; 4}
Das gilt jedoch für alle a, daher noch das Errechnen des Integrals von 0 bis 2.
Wolfram rechnetⅠ= 0,290667 F.E.
Das ist wohl nah genug. Man kann davon ausgehen, dass die anderen Flächenangaben dann auch stimmen.
Bitte beachten: beim Durchintegrieren über eine Nullstelle hinweg subtrahiert sich die Fläche unter der x-Achse!
(falls du diese Rechnung an zwei anderen Stellen ausprobierst, was man ja spaßeshalber machen kann)
Scharf hingucken (Nullstellen und Hochpunkt bei roundabout f(1/2) = 2) und bisschen rumfummeln, dann kommst du auf
f(x) = 1/10*(x+2)*(x+1)*(x-2)*(x-4)
Dann integrierst du eben über die angegebenen Bereiche.
Du musst du irgendwo eine Zehnerpotenz verloren haben. Bei "2 in I eingesetzt" kommen a = 0,099bla raus, also 0,1, nicht 0,01. Dann kommst du auch auf die gewünschten 2,9 FE statt 0,29 FE.
Und ich hatte mit meiner Bauernmethode sogar Recht, obwohl ich die Aufgabe unterschätzt habe. :D