Flächeninhalt mit Integral?

guten Abend, kann mir bitte jemand diese Aufgabe erklären? Die b) habe ich verstanden, die anderen leider nicht. Ich schreibe nächste Woche eine Arbeit und muss das deshalb dringend verstehen. Vielen Dank im Vorraus für jede Antwort!

Answer 1

[Halbrecht]

es gibt wohl auch Verfahren , wie man c) gleich in der gegebenen Form integrieren kann 

Aber es ist ganz klassisch ausmultiplizieren gefordert

1/4 * (x² + 2x - 3) und nun noch mal (x-2)

dann "normal" inte

.

und 2/x² = 2*x^-2

integral daher 

2/(-2+1) * x^(-2+1) =

2/-1 * x^1 =

-2/x 

Answer 2

[evtldocha]

Die b) habe ich verstanden, die anderen leider nicht.

Was ist an der b) anders als an den anderen? Das ist doch immer die gleiche Vorgehensweise bei der Berechnung von Flächen über einem Intervall

• Prüfen, ob Nullstellen im Intervall sind
• Das Integral aufteilen, so dass niemals "über einen Nullstelle hinweg" integriert wird (siehe zu dieser Bedingung auch die unten gezeichnete Skizze der Funktion)
• Beträge aller Teilintegrale aufsummieren.

Aufgabe a)

Prüfen auf Nullstellen:

$\frac{1}{6}x^3-\frac{1}{2}x^2=\frac{1}{6}x^2\cdot\left(x-3\right)\ =\ 0\ \ \Leftrightarrow x_1=0;\ x_2=3$

Damit ist im Intervall von [-1;2] eine Nullstelle und daher:

$A=|\ \int_{_{-1}}^0\left(\frac{1}{6}x^3-\frac{1}{2}x^2\right)dx\ |\ +\ |\ \int_{_0}^2\left(\frac{1}{6}x^3-\frac{1}{2}x^2\right)dx\ |\ =$ $|\ \left[\frac{1}{24}x^4-\frac{1}{6}x^2\right]_{_{-1}}^{^0}|\ +\ \ |\ \left[\frac{1}{24}x^4-\frac{1}{6}x^2\right]_{_0}^{^2}|\$

Skizze: (anhand derer man nun darüber reden kann, wie man das schneller hätte rechnen können, wenn man die Skizze ganz am Anfang gezeichnet hätte und dann das immer funktionierende Rezept oben modifiziert hätte).

Answer 3

[Littlethought]

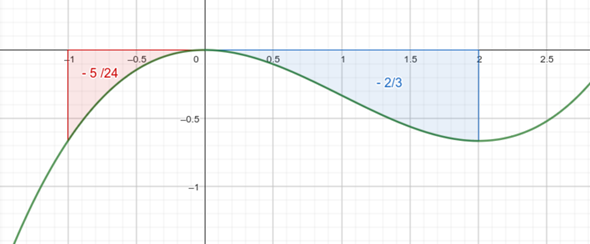
Aufg, 2c Nullstellen: x1 = -3 ; x2 = 1 ; x3 = 2;

Es sind also 2 Teilflächen. Die erste Teilfläche liegt im Bereich-3 < x < 1 oberhalb der x-Achse und die 2. Teilfläche im Bereich 1 < x < 2 unterhalb der x-Achse. Berechne mit Hilfe des Integrals (dazu mußt du den gegebenen Term ausmultiplizieren) diese zwei Teilflächen !

Woher ich das weiß: Berufserfahrung – Lehrer u. Fachbetreuer für Mathematik und Physik i.R.

Comments

[Linnea258]

Danke, die Nullstellen hatte ich schon bestimmt, leider weiß ich nicht, wie man den Term richtig integriert…

[evtldocha]

@Linnea258

Warum redest Du dann von "nicht verstanden", wenn es am Ende eine Frage der Integrationstechnik ist. Das ist extrem ärgerlich, wenn man dann völlig neben der eigentlichen Frage antwortet und somit seine Zeit vergeudet ...

[Linnea258]

@evtldocha

Es hat trotzdem sehr geholfen, da ich mir total unsicher war, ob man die Nullstellen überhaupt so bestimmen kann.