Extremwertproblem?

Hallo🙋🏻‍♀️

Meine Aufgabe lautet:

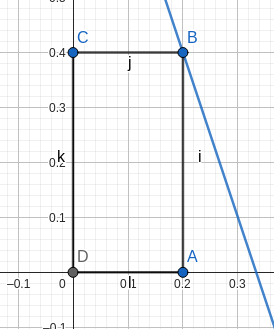
Die rechte obere Ecke eines Rechtecks soll auf dem Graphen der Funktion f(x) = -3x + 1 liegen und die linke untere Ecke im Ursprung des Koordinatensystems. Die Seiten des Rechtecks liegen auf bzw. parallel zu den Koordinatenachsen

a) Erstellen Sie eine geeignete Skizze.

b) Bestimmen Sie die genaue Lage und Größe des Rechtecks mit dem größten Flächeninhalt.

Ich verstehe es leider nicht. Deshalb würde ich euch gerne fragen ob es in Ordnung ist, ob ihr mir den Lösungsweg zeigen würdet mit der dazu passenden Lösung.

Danke im Voraus !!!!!!

LG Hasti

Answer 1

[evtldocha]

Skizze:

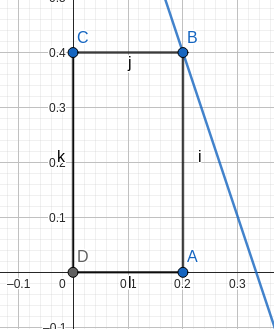
Fläche des Rechtecks:

$A\left(x\right)\ =\ x\cdot f\left(x\right)\ =x\ \cdot\left(-3x\ +1\right)\ =\ -3x^2+x$

Und das ist nun eine Parabelgleichung für die Du das Maximum suchen musst. Also

$A'\left(x\right)\ =\ -6x+1\ =\ 0\ \rightarrow\ x=\frac{1}{6}$

Jetzt kannst in die Flächengleichung A(x) einsetzen und erhältst die maximale Fläche.

$A_{\max}=-\left(\frac{1}{6}\right)^3+\frac{1}{6}=\frac{-1\ +6^2}{6^3}=\frac{35}{216}$

Comments

[hasti06]

muss man dann nicht nach 35/216 dann nullstellen setzen etc?

[evtldocha]

@hasti06

??? - ich habe doch im Schritt davor die Nullstellen von A'(x) gesucht und A(x) ist die gesuchte maximale Fläche für den Wert an x=1/6 an dem die Fläche nach A'(x)=0 maximal ist. Normalerweise würde ich jetzt fragen, ob die Antwort überhaupt gelesen hast.

[hasti06]

@evtldocha

Ah tut mir leid ich habs total verpeilt aber nachdem du die 0 dann nach -6x+1 gestellt hast also -6x+1=0. was genau hast du dann gerechnet also -1 gemacht um dann das auf die andere seite zu bekommen also -6x=1 und dann durch 6. hast du dadurch dieses 1/6 bekommen?

[evtldocha]

@hasti06

Ja, genau so (aber irgendwann sollte eine solche triviale Umformung keine Frage mehr sein, wenn man bereits bei der Lösung von Extremwertaufgaben ist)

[hasti06]

@evtldocha

dann musste es aber x= -1/6 sein. ich habs gerade mit meinem taschenrechner nachgerechnet und mich wunderts gerade wo der fehler liegt

[evtldocha]

@hasti06

Nein -6x+1=0 |-1 -6x = -1 |:-6 ---> x= -1/-6 = 1/6

Lass diese Taschenrechner weg. Die spucken auch nur Falsches aus, wenn man Falsches rein tippt.

[hasti06]

@evtldocha

ah nein ich hab ein fehler gemacht ich hab vergessen vor dem eins ein - zu tun😅😅😅