Differenzialgleichung Trennung der Variablen?

Hallo zusammen,

bei dieser Aufgabe sollen wir die allgemeine Lösung einer separablen DGl. 1.Ordnung mit dem Verfahren Trennung der Variablen bestimmen. Könnte mir jemand dabei helfen und erklären wie man bei solche Aufgaben vorgehen soll.

Aufgabe:

Answer 1

[gauss58]

y' = (y - 7)² * (11x - 26) / (x² - 4x - 12)

Trennung der Variablen:

y' / (y - 7)² = (11x - 26) / (x² - 4x - 12)

dy / (y - 7)² = ((11x - 26) / (x² - 4x - 12)) dx

Partialbruchzerlegung auf der rechten Seite:

dy / (y - 7)² = (6 / (x + 2)) + (5 / (x - 6)) dx

Integrieren:

∫ 1 / (y - 7)² dy = ∫ (6 / (x + 2)) + (5 / (x - 6)) dx

1 / (7 - y) = 6 ln(│x + 2│) + 5 ln(│x - 6│) + C

y = 7 - (1 / (6 ln(│x + 2│) + 5 ln(│x - 6│) + C))

Answer 2

[Rammstein53]

$y' = \frac{(y-7)²*(11x-26)}{ x²-4x-12}$

Substitution: z = y - 7

$(z+7)' = \frac{z²*(11x-26)}{ x²-4x-12}$

Das ist gleichbedeutend mit:

$z' = \frac{z²*(11x-26)}{ x²-4x-12}$

$\frac{z'}{z²} = \frac{11x-26}{ x²-4x-12}$

Wegen z' = dz/dx:

$\frac{1}{z²}dz = \frac{11x-26}{ x²-4x-12}dx$

Linke Seite nach z integrieren, rechte Seite nach x

$\frac{-1}{z} = 6ln(|x+2|) + 5ln(|x-6|)+C$ $z =\frac{-1}{6ln(|x+2|) + 5ln(|x-6|)+C}$

Substitution rückgängig machen:

y = z + 7

$z = 7 - \frac{1}{6ln(|x+2|) + 5ln(|x-6|)+C}$

Answer 3

[Merlin128]

Die Lösung lautet:

​

Comments

[Hana09]

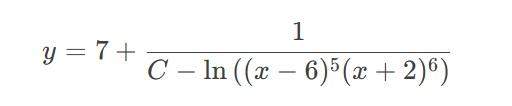
Danke dir, könntest du mir vielleicht sagen wie du darauf gekommen bist