Beispiel fläche integral?
Hallo,
habt ihr ein Beispiel woran man den Zusammenhang von der Fläche und dem Integral erklären könnte ? (Flächenbilanz)
4 Antworten
ein bisschen Bildung vorweg :
Es gibt zwei Zugänge zum Funktion mit dem Namen Integral : Fragt man sich , was die Umkehrung der Ableitung ist , kommt man zum Integral der Funktion
Andererseits hat man entdeckt , dass man die Flächengröße zwischen einer Kurve und der x-Achse mit einer Fkt beschreiben kann . Und siehe da : Da ist das Integral der Fkt.
Das Integral im Intervall a bis b ergibt "nur" eine Zahl :
Will man aber die Fläche von a bis b haben , muss man zuerst schauen , ob in diesem Integral eine oder mehr Nullstellen sind . Berührstellen kann man unberücksichtigt lassen.
Die Zahl gibt die Bilanz aller Flächen an , denn Flächen oberhalb werden als + , unterhalb der xAchse als - angesehen
Das der Grund ist für die Notwendigkeit der Suche nach Nullstellen.
so ist das Int von 0 bis 2pi von sin(x) = 0 , die Flächensumme aber 4 .
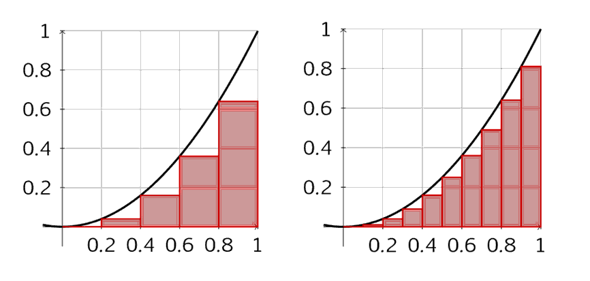
Der Klassiker zur Erläuterung des Unterschieds von Fläche und Wert des Integrals ist die Funktion x³:
Als Integral ergibt sich bei jedem zum Nullpunkt symmetrischen Intervall (in der Skizze von [-1;1]) der Wert 0, da die Funktion symmetrisch zum Ursprung ist und sich das negative Integral links vom Ursprung mit dem positiven Wert des Integrals rechts vom Ursprung zu 0 addiert. Betrachtet man allerdings Flächen, dann muss man die Beträge der Integrale addieren, da eine Fläche nicht negativ sein kann und es erginbt sich der doppelte Flächenwert des Integrals rechts vorm Ursprung (x ≥ 0).
Fazit: Das Integral ist keine Fläche. Die Berechnung von Integralen liefert lediglich eine Methode zur Berechnung von Flächen.

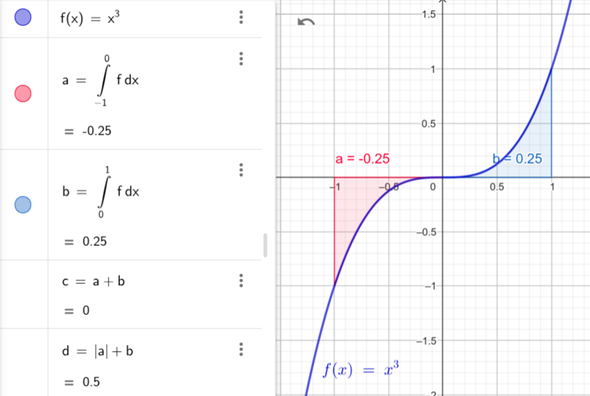
Um den Zusammenhang zwischen dem Integral einer Funktion f(x) und der von der x-Achse und der Funktion eingeschlossenen Fläche zu veranschaulichen, füllt man diesen Bereich mit Rechtecken aus.
Im Bild unten hat man dazu das x-Intervall [0,1] gewählt und fünf Rechtecke der Breite 1/5=0.2. Die Rechteckbreite bezeichnet man mit dx.
Die Höhe eines jeden Rechtecks ist gegeben durch die entsprechenden Funktionswerte f(0*dx), f(1*dx), f(2*dx), f(3*dx) und f(4*dx). Addiert man die Flächen der Rechtecke, erhält man einen Näherungswert für die Fläche, welche f(x) im Intervall [0,1] mit der x-Achse einschließt.
Um diesen Näherungswert zu verbessern, verkleinert man dx auf z.B. 0.1. Man erhält nun 10 Rechtecke und es liegt nahe, dass diese Summe einen besseren Näherungswert darstellt.
Dieses Spiel triebt man jetzt weiter, d.h. dx wird imer kleiner, und die Anzahl der Rechtecke folglich immer grösser. Als Grenzwert erhält man das Integral von f(x) im Intervall [0,1].
Deswegen könnte man das Integral auch so schreiben:
heisst eine Summe unendlich vieler Rechtecke der unendlich kleinen Breite dx über das Intervall [a,b]. Es ist jedoch üblich, anstelle des Summenzeichens das Integralzeichen zu verwenden.