3.45)c?
Wie rechne ich weiter wenn ich mir die x werte berechnet habe?

5 Antworten
Um die Nullstellen zu bestimmen, musst du die Funktion gleich 0 setzen.
Danach x ausklammern und danach den Satz vom Nullprodukt anwenden:
Um das Verhalten im unendlichen zu bestimmen, musst du einfach unendlich bzw. minus unendlich einsetzen.
Hier eine deiner Aufgaben als Beispiel:
a)
Damit ergeben sich zwei bzw. drei Möglichkeiten für die NST.
x=0, wegen des Satz vom Nullproduktes:
und
Beim Verhalten im Unendlichen, setzt Du einfach unendlich bzw. minus unendlich ein.
Hier für dein Beispiel zuerst für den Limes gegen unendlich.
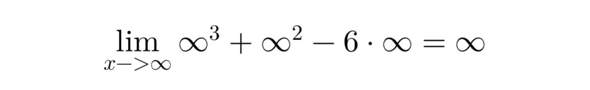
Für -∞ setzt Du einfach für x -∞ ein.
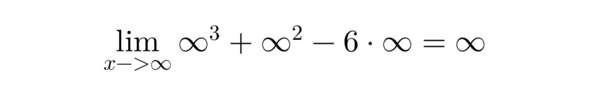
Wieso liege ich im Unrecht? Du solltest dir darüber unbedingt Literatur anschauen.
Mit dieser Methode lässt sich auch die Regel von l‘hospital rechtfertigen. Begründe, warum ich falsch liege!
Ich muss mathematischen Unsinn nicht rechtfertigen! Wenn du eine saubere Definition haben möchtest, dann zeige
∀ T>0 ∃δ > 0 ∀x∈D : x >δ => f(x) > T was äquivalent ist zu
lim f(x) = inf
x->inf
Aber dein Vorgehen oben ist falsch und gäbe an meiner Uni null Punkte.
Wieso knallst du mir jetzt die Definition für stetige Funktion gem. des ε-δ-Kriterium um die Ohren?
Aber trotzdem verstehe ich, was dich aufbringt. Du hättest erwartet, dass ich mit den Eigenschaften der Rationalen Funktionen usw. das begründe. Aber meine Methode hat ja funktioniert.
Das ist nicht die Definition für Stetigkeit auf IR! Diese sieht so aus:
∀x0 € D ∀ε>0 ∃ ẟ > 0 ∀x€D : |x-x0| => |f(x)-f(x0)| < ε
großer Unterschied!
Wie bestimme ich das Verhalten, kannst du mir das auch so aufschreiben bitte
Für das Verhalten im unendlichen ist hier nur der Term mit dem höchsten Exponenten relevant, also -x⁴, da dieser schneller wächst als kleinere Exponenten und bei unendlich großen Werten von x die anderen Terme unwesentlich sind.
Also wie verhält sich Lim(x->∞) -x⁴?
lim(x->∞) -x^4+x³-12x²= lim(x->∞) -x⁴= - lim(x->∞) x⁴ =-∞
Gleiches gilt für -∞, hier wird durch x⁴ der Term gerade und durch -x⁴ wird es -∞
Du klammerst x aus und hast x=0 als eine Nst, dann kannst Du mit der pq-Formel die anderen Nst ggf. ermitteln.
Zuletzt untersuchst Du das Verhalten für lim x -> +unendlich und - unendlich. Fertig
Hinweis: Der Grenzwert eines Polynoms bei Unendlich ist der Grenzwert seines höchstwertigen Terms.
Und wann weiss ich ob -unendlich oder nur unendlich gehört beim ergebnis?
Das habe ich oben gerade geschrieben
Hinweis: Der Grenzwert eines Polynoms bei Unendlich ist der Grenzwert seines höchstwertigen Terms.
und was genau heisst das???
Du wirst sicherlich schon das Thema Grenzwerte/Limes gehabt haben. Wenn Du nicht aufgepasst hast, hast Du ein Problem. - Beim o.g. Beispiel ist x³ der höchste Term, das bedeutet, dass hier der Grenzwert für +unendlich --> (+Unendlich)³=unendlich ist.
Tut mir leid, dass ich bei dem Thema krank war?!
Dann musst Du das nachholen, in der Klausur zählt die Ausrede nicht. Damit gewinnst Du keinen Blumentopf
und was glaubst du mach ich gerade?!!
Du fragst nach einer Lösung ohne eigene Initiative zu zeigen. Eine Anleitung für Dein Problem findest Du in zahlreichen Tutorien im Internet, in Deinem Schulbuch und notfalls kannst Du sicherlich Klassenkameraden fragen. Übrigens steht das ganze erklärt genau darüber (3.43) und darüber ebenfalls.
wenn du die x - Werte der Nullstellen schon hast , dann muss du noch die Nullstellen als NSt1 ( x1 / 0 ) usw hinschreiben.
.
Danach wird nicht mehr "gerechnet" , sondern nachgedacht.
.
a)
wenn x positiv ist und sehr groß geht y f(x) auch gegen +unendlich , weil x³ entscheidend ist .
wenn negativ , dann -unend.
.
b) ist es genau umgekehrt ,weil das Minus vor dem x³ steht .
.
c) überlege selbst
Das Verhalten im Unendlichen ist für ganzrationale Funktionen sehr einfach.
Betrachte z.B:
f(x) = x³-x²+5
Was passiert wenn x --> inf , also die Argumente größer werden?
Nun die Zahl " 5" wird hier nicht viel im Unendlichen ausrichten können, genauso wenig wie die "-x²". Das heißt, dass nur das Verhalten von "x³" eine Rolle spielt.
Wenn x--> inf, dann werden auch die Funktionswerte f(x) --> inf.
Wenn nun x--> -inf , dann wird wegen dem ungeraden Grad von f(x) auch f(x) -> -inf.
Achtung: Diese Betrachtung gilt nur wenn der Leitkoeffizient a > 0.
Danke für die Erklärung, aber verstehen tu ichs leider nicht.
Wann beim Ergebnis dann plus unendlich oder minus unendlich rauskommt.
Schau dir mal f(x) = x² an. Was passiert mit f(x) wenn x--> inf ,also wenn meine Argumente größer werden?
Die Funktionswerte werden also größer und sind unbeschränkt. Das heißt dass das Verhalten von f(x) für x--> inf auch inf, also unendlich ist,
und wo muss ich das einsetzen um es herauszufinden
Du kannst probieren f(10) = 100 ; f(100) = 10000 ; f(1000) = ... usw. Das kann ja nur gegen unendlich gehen.
"Um das Verhalten im unendlichen zu bestimmen, musst du einfach unendlich bzw. minus unendlich einsetzen."
Bitte nicht, nachher macht er das wirklich! Wenn dann sollte man erwähnen, dass einfach die Eigenschaften von den ganzrationalen Funktionen verwendet.