Wie löst man diese Matheaufgabe?
Hallo,
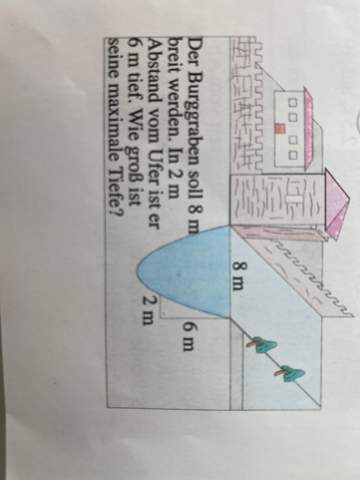
ich habe Probleme die untenstehende Aufgabe zu lösen und wollte fragen, ob mir da jemand helfen kann.
Ich dachte da an einen Lösungsweg mit einem Gleichungssystem, also, dass man erst 3 Punkte bestimmt, die auf der Parabel liegen und mit diesen dann 3 Gleichungen aufstellt. Durch das Subtraktionsverfahren würde man dann die verschiedenen Variablen bestimmen und hätte die Gleichung.
Nun bin ich mir mit den Punktkoordinaten aber nicht so ganz sicher…
Vielen Dank im Voraus für die Antworten!
4 Antworten
Du hast gegeben: f(x)=ax²-c.
Die Nullstellen sind 4 und -4 -> f(4)=0, f(2)=-6
0=a*16-c -> c=16a
-6=a*4-c
-6=4a-16a
-6=-12a
a=0.5
0=16*0.5-c
0=8-c
c=8.
Die maximale Tiefe ist also 8, die Funktion ist:
f(x)=0.5*x²-8
An der Breite, 8m. Lege dir die y-Achse genau in die Mitte des Burggrabens, die x-Achse genau an die obere Grenze.
Also kann man bei der Aufgabe dann einfach davon ausgehen, dass die Parabel nicht nach links bzw. rechts verschoben ist und die y-Achse genau in der Mitte liegt
Ja, das kannst du dir aussuchen, du könntest sie auch anders ins Koordinatensystem legen, das wäre aber komplizierter.
Ok, super :) Danke für die schnelle Antwort!
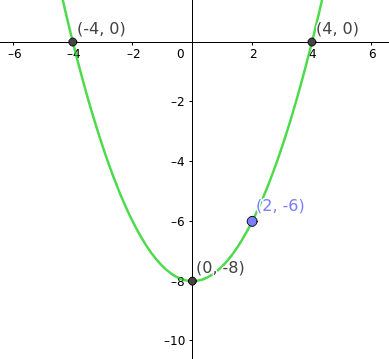
So würde ich die Parabel, den Graben, ins KS legen. Der Scheitelpunkt liegt auf der y-Achse, die x-Achse ist auf Höhe der Wasseroberfläche:
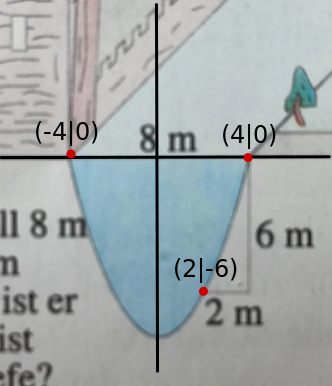
Dann habe ich die Nullstellen bestimmt und die Information, dass 2 m vom Rand der Graben 6 m tief ist, liefert einen weiteren Punkt (2|-6).
Kennst du diese Form für eine Parabelgl?
n_1 und n_2 sind die x-Werte der Nullstellen.
Die beiden Nullstellen einsetzen:
Hier den weiteren Punkt (2|-6) einsetzen um a (Stauchung/Streckung) der P zu bestimmen:
-6 = a•(2 - 4)•(2 + 4
-6 = a•(-2)•(6)
-6 = -12a
½ = a
Die Parabelgl lautet:
y = ½•(x - 4)•(x + 4)
kann man in die Normalform umwandeln (Tipp: bin. Formel):
y = ½•x² - 8
In beiden Fällen für die Tiefenberechnung x = 0 einsetzen:
y = ½•(0 - 4)•(x + 4)
y = ½•(-4)•(4)
y = -8
oder
y = ½•x² - 8
y = ½•0² - 8
y = -8
.
Zeichnung:
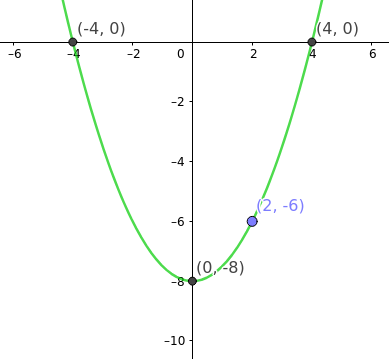
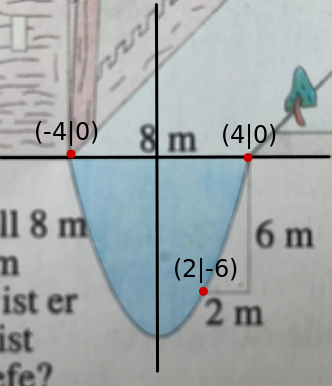
Ich versuche es mal. Was wissen wir?
Allgemein: f(x)=ax^2-b (- weil die Parabel nach unten verschoben ist, der Erdboden soll bei y=0 sein)
Dann gilt aus der Zeichnung:
x = 2 -> y = -6
x = +-4 -> y =0
x = 0 -> y = b (b ist die Verschiebung der Funktion auf der y-Achse)
Wir stellen die allgemeine Funktion nach b um (weil wir das suchen)
b = ax^2 -y
und setzen den Punkt x=4, y=0 ein:
b = a*4^2-0 = 16a (wir haben also b durch a ausgedrückt und damit eine Variable eliminiert)
Wir haben also jetzt: y = ax^2 - 16a
Dort setzen wir jetzt diesen Punkt auf der Parabel ein:
f(2) = -6
-6 = a*2^2-16a = 4a-16a
12a = 6
a=0,5
Damit haben wir a bestimmt, es fehlt uns noch b. Wir wissen aber, dass b = 16a sein muss.
Also ist b = 16*0,5 = 8
Damit hätten wir beide Parameter bestimmt und die gesuchte Funktion lautet:
Probe:
f(2) = -6: 0,5*4-8 = 2-8 = -6 (OK)
f(4) = 0: 0,5*16-8 = 8-8 = 0 (OK)
Damit ist der Graben also 8m tief.
Wenn die Parabel die Form
Y = a* X^2 hat, ist a = 3/2
f(2) = 3/2 * 2*2 = 6
f(4) = 3/2 * 16 = 24
Dein Fehler ist doch aber, dass er bei dir, wenn die Höhe 24 ist, bei 2 aber der Funktionswert 6, ist die Höhe an der Stelle x=2 24-6, also 18 Meter.
Wieso 24-8? Das ist 16. Die Sache ist doch: Nimm an:
f(x)=0.5x². dann hast du:
f(4)=8
f(2)=2. Die Höhe bei 2 wäre also 8-2=6m. So wie die Aufgabenstellung es verlangt. Du hast als Höhe 24m, bei 2 hast du den Wert 6. 24-6=18. Dein Brunnen wäre dort also 18m tief.
Woran erkennt man denn die beiden Nullstellen?