Wie löst man diese Aufgabe mit Hilfe von Strahlensätzen?

Answer 1

[gauss58]

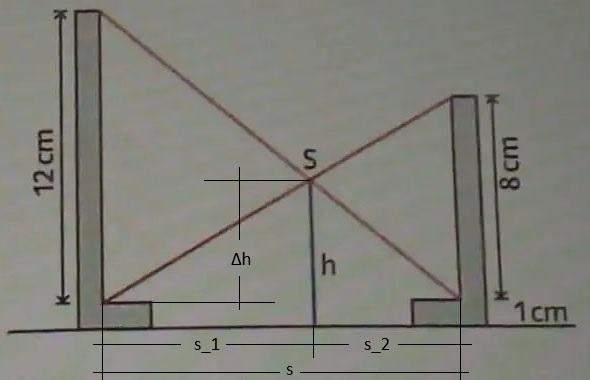
Den Abstand der beiden Stäbe nenne ich ich s, bestehend aus s_1 (Abstand linker Stab nach S) und s_2 (Abstand S nach rechter Stab), also s = s_1 + s_2. Δh ist die Höhe ohne den Sockel.

(1) (s - s_2) / Δh = s / 8

(2) s_2 / Δh = s / 12

-------------------------------

s_2 = (2 / 5) * s

s_1 = (3 / 5) * s

neuer Ansatz:

Δh / ((3 / 5) * s) = 8 / s

Δh = 24 / 5 = 4,8

h = 4,8 + 1

h = 5,8 cm

Ergänzung Skizze:

Dreieck 1: (s - s_2) / Δh = s / 8

Dreieck 2: s_2 / Δh = s / 12

------------------------------------

(1) Δh = (s - s_2) * 8 / s

(2) Δh = 12 * s_2 / s

-----------------------------------

(s - s_2) * 8 / s = 12 * s_2 / s

8s - 8s_2 = 12s_2

s_2 = (2 / 5) * s

s_1 = (3 / 5) * s

Comments

[12345678557]

Danke für die Antwort. Die ersten beiden Schritte habe ich aber nicht verstanden.