Wie löse ich dieses mathematische Problem?
,,Berechne die Oberfläche einer quadratischen Pyramide mit Grundfläche 10 x 10 m und einer Höhe von 4 m. Benutze hierbei den Satz des Pythagoras”.
Brauche dringend eine Antwort komme da nicht weiter!
Was ich bisher habe
3 Antworten
Die Oberfläche der Pyramide setzt sich zusammen aus der Grundfläche und der Mantelfläche. Die Grundfläche ist einfach, das ist einfach die Fläche des Quadrates. Was Du jetzt noch brauchst sind die 4 Mantelflächen. Diese Mantelflächen sind Dreiecke, die Du mit der bekannten Formel berechnen kannst. Was dir noch fehlt ist die Höhe in dieser Formel, da die Grundseite g ja aus dem Quadrat bekannt ist.
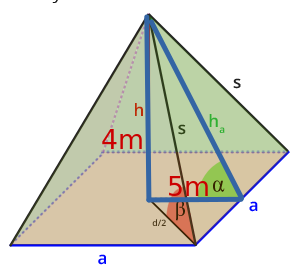
Um an diese Höhe zu kommen, stellst Du dir jetzt ein Dreieck vor, dessen eine Seite von der Spitze der Pyramide bis hinunter zur Grundseite geht. Diese Länge ist zugleich deine gesuchte Höhe. Die errechnet sich dann mit Pythagoras aus einem rechtwinkligen Dreieck, das einmal die gesuchte Höhe als Seitenlänge hat und zugleich die Höhe der Pyramide und die Hälfte der Grundlinie.
Du kommst also nicht weiter, bis wohin kommst du denn?
Die Oberfläche setzt sich aus der Grundfläche und den 4 dreieckigen Seiten der Pyramide zusammen.
Für die Dreiecksflächen benötigst du die Grundseite und die Höhe. Die Höhe (in der Skizze h_a) der Dreiecke musst du dir ausrechnen. Das geht mit dem S.d.P.
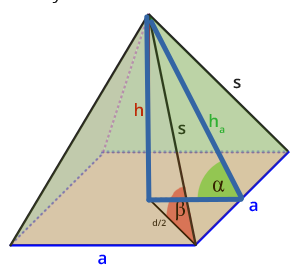
Ich habe dir mal das rw. Dreieck für die Berechnung eingezeichnet.
Pyramidenhöhe h ist eine der Katheten, wie lang die andere Kathete ist, da kommst du selbst drauf. Und h_a ist die Hypotenuse.
Skizze von
https://www.matheretter.de/wiki/pyramide
.
S.d.P.
beschriften der Katheten. Die zweite Kathete hat die Länge a/2 = 10/2 m = 5 m
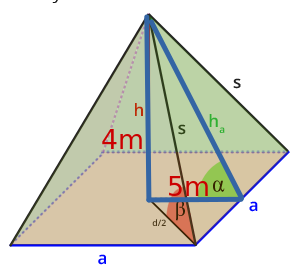
Der S.d.P. lautet also
(4m)² + (5m)² = c²
16m² + 25m² = c²
41m² = c²
6,403... m = c
Die Höhe für die Berechnung der Mantelfläche beträgt rund 6,4 m.
Nun Berechnung der Oberfläche. Die Oberfläche besteht aus der Grundfläche und 4 Dreiecken.
O = G + 4*Dreieck
Die Grundfläche ist ein Quadrat mit der Seite 10 m.
Die Dreiecke haben die Grundseite 10m und die Höhe 6,4 m.
O = (10m)² + 4•½•10m•6,4m
O = 100m² + 2•64m²
O = 228 m²
Wenn man nicht mit 6,4m sondern mit mehr Nachkommastellen rechnet, ist die Oberfläche etwas größer.
Schlag bitte nach, wie man die Fläche eines Quadrats berechnet.
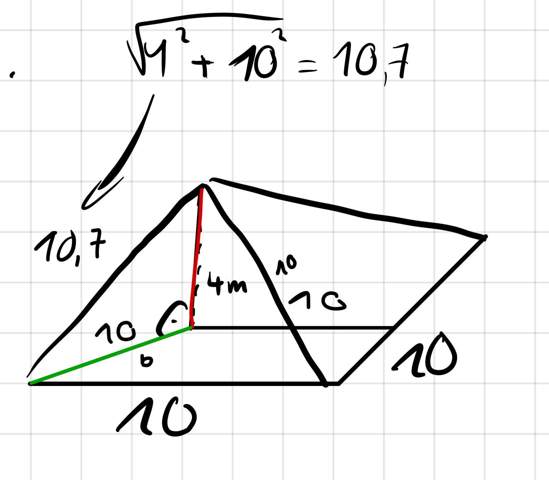
ich hab schon die Seite ausgerechnet hab also Grundfläche 10 m , seite 10,7 m und Höhe 4 m raus und dann hab ich 10 mit 4 multipliziert und dann durch 2 geteilt dann hab ich 20 m*2 raus das mal 4 ist 80 aber das ist viel zu wenig ich brauche eine gestammtfläche von 228,06 so steht es in der Lösung…
Die Höhe h_a ist nicht 10cm oder 10,7 cm.
Die zweite Kathe für den S.d.P. ist nicht 10 cm lang.
Schau dir die Skizze nochmal an oder lies genau, was KuarThePirat geschrieben hat (letzter Satz).
Könntest du mir bitte einfach sagen was ich Rechnen muss sitze schon sehr lange dran bin mit den nerven am Ende
Mache als erstes eine Skizze und überlege dir wie du den Satz des Pythagoras überhaupt anwenden kannst.
Hab ich schon hab auch schon eine Seite raus jedoch weiß ich nicht wie ich die Oberfläche berechnen soll. Die Lösung ist 228,06 aber wie soll ich drauf kommen das ist das Problem
Was ist denn die Oberfläche einer Pyramide. Wenn du eine Seitenfläche schon hast sollte das nicht schwer sein.
Ja aber ich hab’s schon Versuch komme immer auf das falsche Ergebnis irgendwie
Dann stelle bitte deine Versuche hier mit sauberem Aufschrieb ein, dann finden wir gemeinsam den Fehler. Du kannst dazu die Frage ergänzen.
Um die Höhe eines Seitendreiecks zu berechnen gehst du vom Mittelpunkt einer der Grundseiten bis zum Mittelpunkt des Grundflächenquadrates. Wie lang ist diese Strecke? Nicht 10cm. Die zweite Kathete ist die Höhe der Pyramide, die Höhe des Seitendreiecks ist dann die Hypothenuse.
Vielen Dank! Aber warum schreibt man (10)hoch 2? und bei dem anderen nicht