Matheaufgabe Satz des Pythagoras?
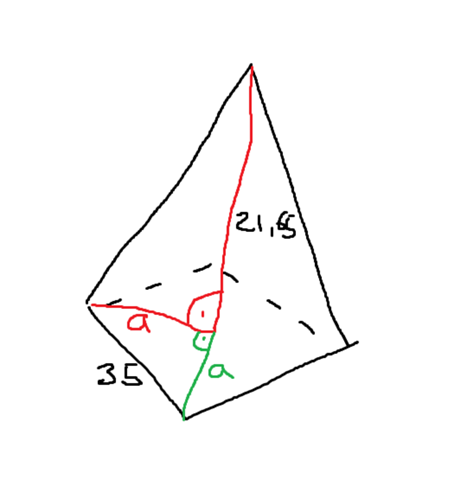
Im Innenhof des Louvre in Paris befindet sich eine 21,65m hohe Glas Pyramide mit quadratischer Grundfläche. Die Seitenlänge der Grundfläche beträgt 35m. berechne die Länge der Kanten der Pyramide also die Länge der Strecke von einer der Ecken der quadratischen Grundfläche zur Spitze
2 Antworten
Da die Grundfläche quadratisch ist, kannst du die Strecke zwischen einer Ecke und dem Mittelpunkt der Basis mit dem Satz des Pythagoras schon berechnen, da es ja ein Dreieck mit einer 35 m langen Hypotenuse und zwei gleich langen Katheten bildet. Die modifizierte Formel ist also: a² + a² = 35², wobei a dann danach eine notwendige Kathete ist, die du für die Lösung der Aufgabe brauchst. Nun nimmst du nämlich diese und die Höhe als andere Kathete und berechnest die Hypotenuse, welche dann c² = a² + 21.65² ist.
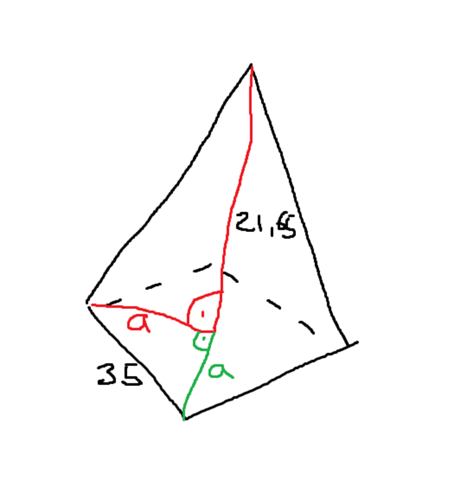
Herauskommen sollten ca. 32.9 m.
Du hast die Höhe gegeben (21,65m) und die Seitenlängen der Grundfläche (alle 35 m)
Jetzt musst du nur noch das ganze in die Formel a hoch 2 + b hoch 2 = c hoch 2 bringen.
Ich denke da wären dann 21,65 hoch 2 + 35 hoch 2 = Seitenlänge hoch 2 richtig.
Vergiss nicht die Wurzel des Ergebnis (21,65 hoch 2 + 35 hoch 2) zu ziehen denn es heißt ja = c hoch 2 und du willst ja einfach nur die Zahl "c" haben in dem Falle.
Ich hab die Aufgabe falsch verstanden, diese Lösung ist falsch!! Entschuldige bitte!!